原来那个文章里面全都是瑇码和公式，充斥了4700多行，卡到已经几乎无法编辑了，所以新开一个文章。

如果笔者有什么写得乱七八糟或者听天书的地方，可以直接评论区开D，笔者即刻更改，以免贻害后人。

2021-01-09：愉悦滚去whk，本文应该长期不更了（咕）
2021-01-17：爬回机房重新阅读了一下本文，修了大量语文锅

SAM

_写在最前：网上最主流的讲解方式无非是 endpos - 构建方法 - 应用，这里也不另辟蹊径，但是会扔掉一些晦涩难懂的证明，争取用阳间一点的语言说罢_

“将所有是旧串后缀且在其后面加c形成的新字符串不是旧串子串的字符串往新串的最长后缀所属节点连一条边。”

如果要求您在一张图上表示一个字符串的所有子串，那么您可能会建一棵 $\texttt{Trie}$ 。

如图：

很有精神的一个 $\texttt{Trie}$ ，从根结点往下，走到任意一个点的 路径 都是原串的一个子串。

但是缺点貌似也很明显，他太占空间了，这框出的这两部分是一模一样的。这是坏的。

我们意识到需要有一种好的存图规则，来尽可能优化我们的空间。

于是乎， 先 辈 们想到了一种氡氡—— $endpos$ 。

$endpos$ ？

假设我有一个字符串 $\mathtt{shenmadongdong}$ 。（这个字符串一听就很巨）

我们截取出一个子串 $\mathtt{dong}$ ，若以一个字串的 最后一位 来表示位置的话，它出现在 $\{10,14\}$ 两处。

我们就将 $\{10,14\}$ 这样的 位置集合 称做 $\mathtt{dong}$ 这个子串的 $endpos$ 。

未来或现在的 IOIAKer 您一定看出来了，这个 $endpos$ 有些十分美妙的性质，这里分别阐述：

_以下钦定 $len_a\leq len_b$_

性质〇：对于一个子串的后缀们，越长的后缀所拥有 $endpos$ 集合越小，反之则反之。

算不上性质的性质/jy

这不是显然的事情嘛？越长的后缀它出现的次数肯定越少哇。

$\Box$

性质一：如果两个子串的 $endpos$ 有相同的元素，则一个中的子串必然为另一个的后缀

我们说过，一个子串的出现位置，由他的 最后一位 表示。

胡乱猜结论：只有最后 $len_a$ 位一样的两个串，才会共享一样的 $endpos$ 。

尝试证明：要是在 $len_a$ 位内出现了不同的某一字符，那么他们的最后一位必然 落不到同一个位置 ，那么他们的 $endpos$ 内的元素必然不同。

$\Box$ （好感性啊 AwA ）。

性质二：两个子串 $a,b$ ，要么其中一个的 $endpos$ 包含另一个的，要么两者的 $endpos$ 没有交集。

如果 $a$ 是 $b$ 的后缀，那么 $b$ 出现的地方 $a$ 必然也出现了，那么 $endpos(b)\subseteq endpos(a)$ 是显然的。

如果不是，那么根据性质一，二者不会有交集。

$\Box$ （这个就非常有理有据）（确信） 。

性质三：如果把所有 $endpos$ 集合完全相同的子串归在一个等价类里，那么每个 $endpos$ 的等价类里的子串长度连续。

这个性质十分好用。这证明起来也是很 $naive$ 的。

如果存在 $a,b$ 归在同一个等价类里，且 $len_a+1<len_b$ （也就是中间出现了断层）。

根据性质一， $a$ 必为 $b$ 的 后缀 。

根据性质〇，更短的后缀都和 $b$ 出现的位置 完 全 一 致 了，那更长的后缀怎么说也更应该一样了 QwQ。

但既然如此，比 $a$ 再长一位的后缀凭什么不能和 $a,b$ 在同一个等价类里？这不公平。

$\Box$ （鬼扯证明）。

插播：$parent\ tree$ ？

虽然性质还有很多，但是这时的确就应该开始讲 $parent\ tree$ 了，这的确符合认识算法的客观规律。

我们看 $\mathtt{shenmadongdong}$ 中的 $\mathtt{n}$ ，它的 $endpos$ 为 $\{4,9,13\}$ 。

如果我们要往它前面加一个字符，我们有 $\mathtt{en}$ 和 $\mathtt{on}$ 两种加法，他们的 $endpos$ 分别为 $\{4\}$ 和 $\{9,13\}$。

你灵光一现，意识到在一个字符串 前面 加一个字符，很可能就会把原来这个字符串的 $endpos$ 分割成若干份 。

我们接着在 $\mathtt{on}$ 上加字符，此时只有一种加法 $\mathtt{don}$ ，$endpos$ 依然是 $\{9,13\}$ 。

你完善了你的猜想，所谓的 “分割成若干份” 也可以指的是 一份 。当加字符后和原来还是在 同一个等价类 里的话，就会出现这种情况。

我们接着在 $\mathtt{don}$ 上加字符，此时又有两种加法 $\mathtt{adon}$ 和 $\mathtt{gdon}$ ，分别有 $endpos$ 为 $\{9\}$ 和 $\{13\}$ 。

这更加证实了你的猜想，即：

『一个字符串 前面 加一个字符，将会把原来这个字符串的 $endpos$ 分割成若干（可能为一）份 』

多么伟大不朽的成就。

我们称这是『神马氡氡第一定律』 。

根据性质二，非后缀关系的两个子串 $endpos$ 无交集，所以以 等价类作为结点 ，这些分割关系构成了一些 树形结构，即一棵森林。

森林算不上 $\mathbf{tree}$ ，我们需要一个超级根来聚合一棵树，不难想到，空串所在的等价类 正符合当超级根的要求 。因为他无处不在，所以他的 $endpos$ 是 $\{1,2,3,4,5,6,7,8,9,10,11,12,13,14\}$ ，相当于全集。

下属其它的 $endpos$ 集合，都是这个集合的子集。

那么我们这就构建出了一棵 $parent\ tree$ ，对于 $\mathtt{shenmadongdong}$ 这个仙气溢出的字符串，我们能构建这样一棵 $parent\ tree$ ：

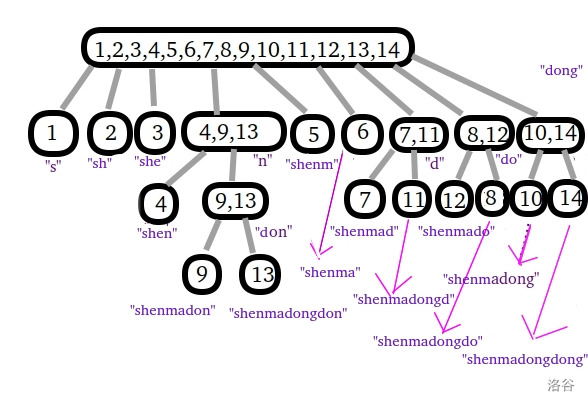
这里引入一个概念：我们称某个等价类中的 最长子串 指的是： （$endpos$ 符合某个等价类） 的所有子串中，长度最长的那个子串。

最短子串 的定义同理。

这里用 $\color{purple}{\texttt{给}}$ 指导最爱的颜色标出了“每个结点对应的等价类的 最长子串 ”。

结点中的数字表示的是 $endpos$ 集合。

性质四：如果两个等价类 $A,B$ ，在 $parent\ tree$ 上 $B$ 是 $A$ 的父亲 ，那么 $B$ 的最长子串的长度+1，一定等于 $A$ 的最短子串的长度。

奇怪的性质增加了.jpg

我们再次 YY 一下 $parent\ tree$ 的构造规则：

在一个等价类中的某个子串前再 添加一个字符 。

不难发现，若选择的这个子串是这个等价类中的 最长子串 ，形成的字符串就必然归于其 儿子 的等价类。否则就仍在这个等价类中。

如果选择的是最长子串，那这个新形成的字符串肯定这个 儿子等价类 中 最短 的一个。

$\Box$

算法可行性不证了，版（zuo）面（zhe）有（tai）限（cai）。

看到这里，您必然会想：“我是来看 SAM 的，这个吊人却给我讲些什么 $parent\ tree$ 之类的东西搞啥呢。”

我们将要构建的SAM，就和 $parent\ tree$ 有一样的 结点 定义。

事实上，SAM 的前置知识还是很重要的，了解了这些性质就有效地避免了全文背诵的惨案。

字符串数据结构的全文背诵是最不彳亍的，因为出出来的那些题大多需要 魔改 数据结构的机体，光是全文背诵就很痛苦了。

构建一台后缀自动姬

$Step\ 0$：有关变量

首先我们需要整出一套自动姬所需的数组啊啥的。

东汉末名将赵子龙就曾说过：“能进能退 （能伸能缩），乃真正法器。”

我们需要让我们的字符串能向前扩展，也能向后扩展，以表达所有的子串。

我们已经有了在子串 前面 加字符的方法，即 $parent\ tree$ 的构造规则。

再放送 $parent\ tree$ ：

我们用存 $fa$ 的方式维护这棵 $parent\ tree$ ，$fa[u]$ 里存的是它在 $parent\ tree$ 里面的 直接父亲 。

用 $endpos$ 等价类的知识解释，就是 $u$ 等价类的 最长子串 ，它最长的那个 （不同等价类 的后缀）所在的等价类。比如上图中的 $\mathtt{shenmadon}$ 所在等价类的 $fa$ ，就是 $\mathtt{don}$ 所在等价类。

上面是在前面加字符的方法，那么在其后面加字符的方法呢？

我们用 $ch[u][c]$ 来表示：在$u$ 结点 对应的等价类 的 最长子串后面 加上一个字符 $c$ ，形成的新字符串所属的等价类 对应的结点 。（参考 $\mathtt{Trie}$ 上的连边）

你搁着读绕口令呢？/fn

你可能需要多读几遍格物致知，更口区的还没来呢。

_/ *这里讲的不好被小猫 @Schwarzkopf_Henkal D了，所以加一个例子 * /_

举个栗子，假设我们的 $\mathtt{shenmadon}$ 属于的等价类在 $u$ 结点，我们在后面加上 $\mathtt{g}$ 变成 $\mathtt{shenmadong}$ ， $\mathtt{shenmadong}$ 归在等价类 $v$ ，那么我们有 $ch[u][‘g’-‘a’]=v$

其实和 这道题 表达的意思差不多。

$ch$ 数组和 $parent\ tree$ 没有什么直接关系，它不过是自动姬体内的一些连边。或者说我们要维护两个数据结构，一个是 $fa$ 维护的 $parent\ tree$ ，一个是 $ch$ 维护的SAM姬体。

我们现在有了能伸能缩的方法，接下来就可以开始建造后缀自动姬辣！

_以下不再区分结点和结点所对应的等价类，这两个是同一个氡西_

$Step\ 1$：构建前的准备工作

我们需要明晰构建自动姬的方法为 增量法 。

简单点说就是自动姬每次吞进 一个字符 ，应对这个字符改变内部结构，再吞进下一个字符，以此往复。

每次吞字符的行为之间需要传递一些信息，除了以上提到的 $fa$ 和 $ch$ 照例保留外，还需要传递一个 $lst$ 变量，表示上一次 添加字符后的串 $s$ 所属的等价类。

显然，上一次加完字符后的串 $s$ ，一定是 $lst$ 这个等价类的 最长子串，这不难理解，毕竟 $s$ 甚至是目前所有子串中最长的一个，自然在它的类里也当人上人。

我们在最长子串 $s$ 后加上了一个字符 $c$ 形成了一个新串，根据性质四，我们知道这个新串将会归到一个 新的等价类 里。

所以我们开一个新点 $np$ ，表示 $s+c$ 所属的新等价类对应的结点。

如果我们称 $len(u)$ 为 $u$ 这个等价类 最长子串的长度 。暂时地，我们应使 $len(np)=len(p)+1$ ，因为 $np$ 目前的最长子串是由 $p$ 的最长子串加上 一个 字符 $c$ 变成的。

举个例子，我们当前构建到了 $\mathtt{shenmad}$ ，它在 $endpos$ 集合 $\{7\}$ 里当人上人。

我们在它后面加一个字符 $\mathtt{o}$ ，显然，新串 $\mathtt{shenmado}$ 和原串已经不在同一个等价类中了，他早已成为 $\{8\}$ 集合的 最长子串 了。

这部分的瑇码～（人生苦短，我用结构体）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
struct node
{
	int len, fa;
    //len——最长子串长度,fa——（最长的（不同等价类的）后缀）所在的等价类
	int ch[27];
	node()
	{
		memset(ch, 0, sizeof(ch));
		len = fa = 0;
	}
} T[MAX << 1];
int lst = 1, tot = 1;
void add(int c)
{
	int p = lst;//取出当前最长子串所在等价类
	int np = ++tot;//开一个新点
	T[np].len = T[p].len + 1;//新等价类的len等于原等价类len+1
	lst = tot;//更新最长子串所在类
	......
        
}
signed main()
{
	string s;
	cin >> s;
	int len = s.length();
	for (int i = 0; i < len; i++)//增量法
	{
		Tree.add(s[i] - 'a');
	}
	......
}
$Step\ 2$：遍历新串后缀，到第一个出现过的子串为止

每当我们加入一个新字符，可能之前某些子串的 出现位置（即 $endpos$ 中的元素）就会变多。

具体地说，如果我们当前加到第 $n$ 位，有些新子串从来 没出现 过，需要多开一个 $\{n\}$ 等价类包含它们；有些新子串 曾经出现 过，它们的 $endpos$ 中就多一个 $n$ 。

我们需要找到这些新子串的出现位置。

这样的新子串满足什么性质呢？很简单，一定是 加字符之前 的原字符串的某个 后缀 ，再拼接上我们 现在加的这个字符 $c$ 。（所谓 $endpos$ 者，你甚至都不以 $c$ 为 $end$ ，凭什么让他给你贡献 $endpos$ 呢，这不公平。）

既然是后缀关系，对于拼上 $c$ 的新串，一定存在某一长度的后缀，使得长度 小于 它的其它后缀都出现过。

举个例子，我们的原字符串为 $\mathtt{shenmadongdo}$ ，现在我们加上一个字符 $\mathtt{n}$ ，定然只有 $\mathtt{shenmadongdon,henmadongdon,enmadongdon,\dots,don,on,n,}\varnothing$ 这些串的 $endpos$ 可能会改变。

这其中，只有长度小于 $\mathtt{don}$ 的后缀（$\mathtt{don,on,n,}\varnothing$）的 $endpos$ 将在原有基础上加上 $13$ ，其它的后缀都将归在 $\{13\}$ 这一类中。

这就需要我们从左往右遍历后缀，找到这个第一个出现过的后缀。

我们知道，根据『神马氡氡第一定律』，一个字符串 前面 加一个字符，将会把原来这个字符串的 $endpos$ 分割成若干（可能为一）份 ，在 $parent\ tree$ 上，表现为 下分出几棵子树 。

古语有云：“水能载舟，亦可覆舟（亦可赛艇）”。

这启示我们我们以相反的方面看这一定律。（胡扯）

我们也可以说一个字符串 前面 删掉几个字符 ，在 $parent\ tree$ 上，表现为 向上跳 $fa$（或原地不动） 。

我们称这是『神马氡氡第一引理』。

那么，一种十分女少的遍历后缀方法就呼之欲出了：在 $parent\ tree$ 上，向上跳 $fa$ 。

我们再再放送 $parent\ tree$ ：

（越看越丑）

以 $\mathtt{shenmadon}$ 为例，我们向上跳一级 $fa$ ，遍历到后缀 $\mathtt{don}$ ，相当于在字符串前面删掉了 $6$ 个字符。再跳一级 $fa$ ，遍历到后缀 $\mathtt{n}$ ，相当于在前面删掉了 $2$ 个字符。

这时，您可能会疑问，这样遍历后缀，难道不会漏掉很多在同一等价类里的后缀吗？这是好的。

我们说，遍历的作用，在于找到 第一个出现过的后缀 。

属于同一等价类的子串们，它们 $endpos$ 相同，在原串中的 出现情况 也相同。所以，我们只需查看每个等价类中的 一个串 （这里选用 最长子串 ），即可判断整个等价类是否曾经出现 。

高明！

至于实现，看看瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

/*遍历后缀*/
while (p && !T[p].ch[c])//前面的p可以单纯地看做防止它跳出SAM
//后面的则是看（p的最长子串+c字符）是否曾经出现
{
	T[p].ch[c] = np;//若未曾出现，则（p的最长子串+c）归于{n}这个等价类里
	p = T[p].fa;//跳fa，遍历下一个后缀
}

if (!p)//若之前是因跳出SAM而结束，那么说明（∅+c）=c 这个字符都从来没出现过
{
	T[np].fa = 1;//看来{n}这个集合需要连接超级根1。
	return;
}
$Step\ 3$：自动姬的处理计划一

还记得的吧，T[p].ch[c] 指向的是一个 等价类 。

假设我们已经用以上手段得到（某个长度的后缀+c）所处的 等价类（它就是上面瑇码中的 T[p].ch[c] ），能走到这里，说明这个后缀是第一个曾出现过的后缀。

设 $q=T[p].ch[c]$ ，我们需要知道 （ $p$ 的最长子串 + $c$ ） ，是否就是这个 $q$ 的 最长子串。这决定着我们该如何修改自动姬的结构。

看来我们需要 $\mathbf{dark}$ 力分讨这个问题。

最凑巧的情况当然是（ $p$ 的最长子串 + $c$ ）就是 $q$ 的最长子串。

嘛，既然这个串是最长子串，那么根据性质二，显然，同等价类的其它子串们都将是它的 后缀 。

而我们之所以会揪出这个子串来，是因为这个最长子串的 $endpos$ 集合需要 增添 一个 $n$ 。那么根据性质一，它的 后缀 们也会增添一个 $n$ 。

那么我们直接令这整个集合 $q$ ，成为 $np$ （它对应 $\{n\}$ 等价类）的 $fa$ 即可。

为什么？根据『神马氡氡第一定律』，$q$ 中增添一个 $n$ ，即 $q$ 的等价类能够额外 分割 出一个 $\{n\}$ 等价类 ，即在 $parent\ tree$ 上 $q$ 成为 $np$ 的 $fa$ 。

只需一步操作即可，最终的形态依然保证符合性质。这好吗？这很好。

举个例子，我们当前已经处理到了 $\mathtt{shenmadongdon}$ ，正是大业将成的时候。此时我们应该在后面加上一个 $\mathtt{g}$ ，经过 $Step\ 1$ 的准备，我们开了一个新点 $np$ ，等价类为 $\{14\}$ ，最长子串为 $\mathtt{shenmadongdong}$ 。

经过 $Step\ 2$ 的遍历，我们最终在 $\mathtt{don}$ 这个后缀所处的等价类 $p$ 上停了下来，这个 $\mathtt{don}+\mathtt{g}$ 之前已经出现过了。

我们把 $\mathtt{dong}$ 所在的等价类 $ch[p][‘g’-‘a’]$ 取出来记作 $q$ ，当时这个等价类的最长子串恰好就是 $\mathtt{dong}$ ，于是我们让 $np$ 的 $fa$ 等于 $q$ ，构建出一棵 $parent\ tree$ ：

（上面描述的操作发生在图上的最右侧，即 $\mathtt{shenmadongdong}$ 所处等价类（$np$）的 $fa$ ，连向 $\mathtt{dong}$ 所处等价类（$q$））

这部分的瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

if(!p)
{
	......
}//上接上文
else
{
	int q = T[p].ch[c];//取出 q 这个等价类
	if (T[q].len == T[p].len + 1)//这里是一个转化过的判断条件
    //经过性质四的转化，这句话相当于：q的最长子串=p的最长子串+c
	{
		T[np].fa = q;//q成为 np（即{n}）的 fa
        
	}
	......
}

$Step\ 4$：自动姬的处理计划二

东坡居士曾写道：“人有悲欢离合，月有阴晴圆缺，此事古难全。”

有一说一确实，不可能每次加一个字符都能变出某个等价类的最长子串，不然您的欧气也钛好了。

我们需要进一步考虑 不是最长子串 的情况。

神 @华莱士 大佬提供了一个妙妙妙的理解方法。

我们用下三角图表示一个字符串的后缀们：

当前我们的原串是 $\mathtt{shenmado}$ 。

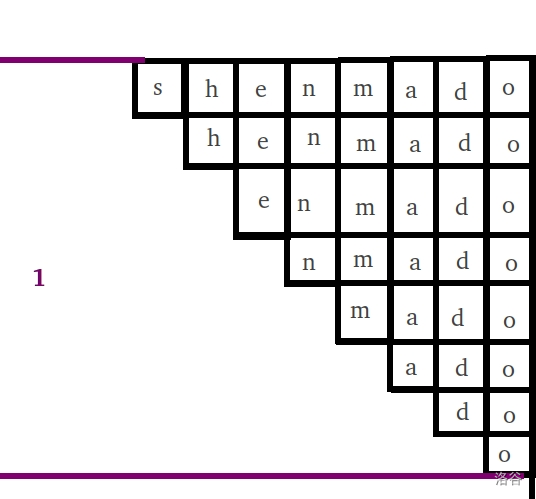
图中用 $\color{purple}{\texttt{给}}$ 指导最喜欢的颜色标出 后缀所属的等价类 。当前这些后缀都归在同一个 $endpos=\{8\}$ 的等价类中。

我们此时将要添加一个字符 $\mathtt{‘n’}$ ，根据 $Step\ 2$ 的遍历，它停在了 $\varnothing\mathtt{+n}=\mathtt{“n”}$ 这个后缀上。

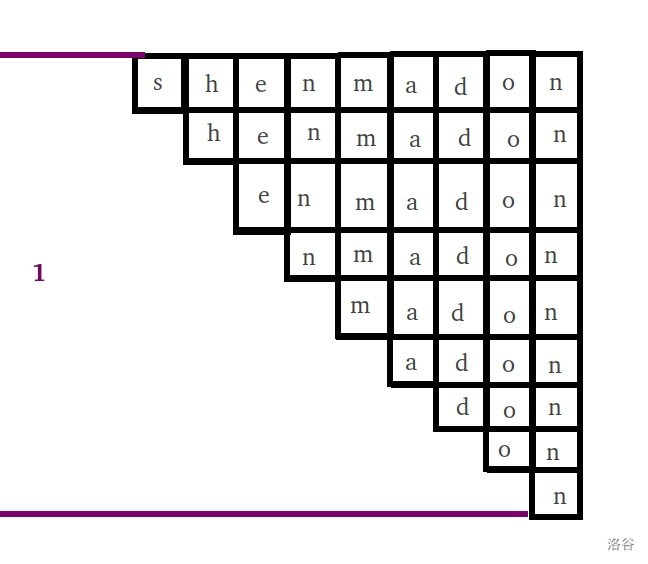
按照早已设想的道路，$\mathtt{n}$ 这个子串所在等价类的 $endpos$ 应当原先的基础上 添加 一个 $9$ ，变成 $\{4,9\}$ 。而其它的后缀 $\mathtt{don,adon}$ 之类的应当归于 $\{9\}$ 。

对于等价类的定义，要求类内的 $endpos$ 相同，但现在我们发现这么一搞以后，现在这个等价类的 $endpos$ 不尽相同了。也就是说，我们需要把它 裂开 来，分裂成两个等价类，一部分为 $\{9\}$ ，另一部分为 $\{4,9\}$ 。（即：一部分是曾经出现过的，一部分是曾经没出现过的）

以上就是当（ $p$ 中最长子串 + $c$ ）不是 $q$ 中最长子串的大致处理提纲/cy。下面我们来康康细节。

我们分裂也不能白嫖空间啊，我们需要新创建一个结点 $nq$ ，来表示拆分出的两部分中，曾出现过 的那一部分（这里指图上的 $2$ ）。

之前的瑇码里我们看到，一个结点它有三个属性，$ch,fa,len$ ，我们来康康 $nq$ 需要具备怎样的属性。

首先看 $ch$ ，它表示的是在 后面 加字符后归在的等价类，肉眼观察法可得，$ch[nq]$ 和原来 $ch[q]$ 其实没有区别。那么 直接继承 $q$ 的 $ch$ 就是了。

为什么？ $nq$ 在分裂以前与 $q$ 的差别在且仅在于 $endpos$ ，而在后面加一个字符能转移到哪里，就不在 $endpos$ 决定的范围内了。

然后看 $len$ ，在 $Step\ 2$ 中 $p$ 不断跳跳跳最后跳到了新串的某个 曾经出现 过的后缀。这个曾经出现的后缀属于的结点是 $q$ ，以 （当前 $p$ 的最长子串+c）的 长度 为界限，将分裂出了一块 $nq$ ……

那么显然，$nq$ 的 $len$ 等于（当前 $p$ 的最长子串+c）的长度，也就是 $len(nq)=len(p)+1$ 。

最后是 $fa$ 。$fa(q)$ 之前和 $q$ 在树上成父子关系，根据性质四，当时的 $len(fa(q))+1$ 必然等于 $minlen(q)$ ，也就是论 长度 而言，原 $len(fa(q))$ 与 $minlen(q)$ 紧密相接。

分裂后，$minlen(q)$ 必然被归到了 $nq$ 类里，所以 $nq$ 与原 $fa(q)$ 紧密相接，所以 $fa(nq)=fa(q)$。

同时，$nq$ 是从 $q$ 上 拆分 下来的，且 $nq$ 的 $len$ 小于 $q$ ，根据性质〇和一些推理， $nq$ 得变成 $q$ 的新 $fa$ 。

看上去就像一个链表的插入？

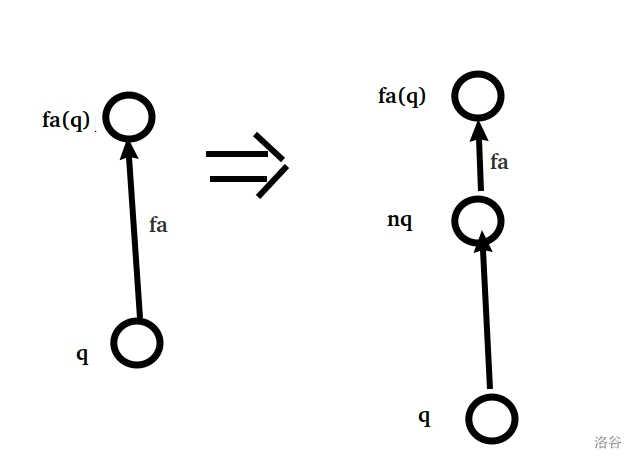
但是我们还有一个非常严肃的问题存在，有些结点的 $ch[c]$ 指向的是 $q$ ，但是当我们分裂后，这些 $ch[c]$ 需要指向 $nq$ 。这就非常难搞，我们需要将 $ch$ 重定向 。

具体操作方法，我想先放瑇码：

1
2
3
4
5
while (p && T[p].ch[c] == q)
{
	T[p].ch[c] = nq;
	p = T[p].fa;
}

……

这个靓仔是不是在哪里见过？

我们把之前遍历后缀的瑇码部分拿出来对比：

1
2
3
4
5
while (p && T[p].ch[c] == 0)
{
	T[p].ch[c] = np;
	p = T[p].fa;
}

发现相同之处了吧，这说明我们的重定向其实也同时在做一个 遍历 $p$ 的后缀 的工作。我们对这些遍历到的 后缀 进行重定向，这些后缀的 $ch[c]$ ，需要满足原先指向 $q$ 。

以上就是自动姬躯壳的全部组件，我们组装起来观赏一下完整瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

/*Step 1*/
struct node
{
	int len, fa;
	int ch[26];
	int siz;
	node()
	{
		siz = len = fa = 0;
		memset(ch, 0, sizeof(ch));
	}
} T[MAX];
int tot = 1;
int lst = 1;


void add(int c)
{
	/*Step 2*/
	int p = lst;
	int np = lst = ++tot;
	T[np].len = T[p].len + 1;
	while (p && T[p].ch[c] == 0)
	{
		T[p].ch[c] = np;
		p = T[p].fa;
	}
	if (!p)
	{
		T[np].fa = 1;
	}
	else
	{
    	/*Step 3*/
		int q = T[p].ch[c];
		if (T[q].len == T[p].len + 1)
		{
			T[np].fa = q;
		}
        
        /*Step 4*/
		else
		{
			int nq = ++tot;
			T[nq] = T[q];
			T[nq].len = T[p].len + 1;
			T[q].fa = T[np].fa = nq;
			while (p && T[p].ch[c] == q)
			{
				T[p].ch[c] = nq;
				p = T[p].fa;
			}
		}
	}
}

简单应用

判断一个串 $A$ 是否是另一个串 $B$ 的子串

真就把 SAM 当成AC自动姬来用呗。

对 $B$ 建一棵SAM，一个一个吞进 $A$ 的字符，每吞进一个字符，在 SAM 上走对应的 $ch$ 边。（因为 $ch$ 的本质就是在一个串的后面加字符）。

没有板子。

本质不同子串个数

我们知道 SAM 结点的一个很 $\mathbf{dark}$ 的特点：它代表的是一整个 等价类，并且根据性质二，它们之间 没有交 。

这样我们大致有了个口胡想法，对 等价类大小 求和，这样可以做到不重不漏。

那么怎么求和呢，细化地说，我们如何知道一个等价类里有多少元素呢？

根据四， $minlen(u)=maxlen(fa(u))+1$ ，又因为类内长度 连续 ，那么，类内元素个数 $n=maxlen(u)-(maxlen(fa(u))+1)+1=maxlen(u)-maxlen(u)$ 。

那么只需统计 $\sum(maxlen(u)-maxlen(u))$ 即可～

板子题一：P2408 不同子串个数

放一下瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAX = 1e5 + 7;
struct node
{
	int ch[27];
	int len, fa;
	node()
	{
		len = fa = 0;
		memset(ch, 0, sizeof(ch));
	}
} T[MAX << 1];
int sum = 0;
struct SAM
{
	int tot = 1, lst = 1;
    /*SAM 组件*/
	void add(int c)
	{
		int p = lst;
		int np = lst = ++tot;
		T[np].len = T[p].len + 1;
		while (p && T[p].ch[c] == 0)
		{
			T[p].ch[c] = np;
			p = T[p].fa;
		}
		if (p == 0)
		{
			T[np].fa = 1;
		}
		else
		{
			int q = T[p].ch[c];
			if (T[q].len == T[p].len + 1)
			{
				T[np].fa = q;
			}
			else
			{
				int nq = ++tot;
				T[nq] = T[q];
				T[nq].len = T[p].len + 1;
				T[q].fa = T[np].fa = nq;
				while (p && T[p].ch[c] == q)
				{
					T[p].ch[c] = nq;
					p = T[p].fa;
				}
			}
		}
		sum += (T[np].len - T[T[np].fa].len);//统计
	}
} Tree;
int N;
signed main()
{
	cin >> N;
	for (int i = 1; i <= N; i++)
	{
		char c;
		cin >> c;
		Tree.add(c - 'a');
	}
	cout << sum << endl;
}

板子题二：[SDOI2016]生成魔咒

同，瑇码不放了。

获取两个串的最长公共子串的长度

对于其中任意一个串（称为原串）建SAM，像子串判别一样，一个一个吞进另一个串（称为匹配串）的字符。

但不同的是，子串判别是一旦没有了 $ch[c]$ 的转移就返回 0 ，而获取公共子串则是 “遇事不决先跳 $fa$ ”，相当于在前面 删掉一些字符 ，再尝试转移一下。同时根据转移到的位置，实时更新当前匹配长度 $cur$ 。

当一个字符处理完后，记当前 $cur$ 为 $maxl[i]$ ，表示从匹配串的第 $i$ 位 向前，两串最长匹配了多长。

最终的答案就是 $maxl$ 中最大的一个。

板子题：SP1811 LCS - Longest Common Substring

放一下瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <bits/stdc++.h>
using namespace std;
const int MAX = 3e5 + 7;
struct node
{
	int len, fa;
	int ch[26];
	node()
	{
		len = fa = 0;
		memset(ch, 0, sizeof(ch));
	}
} T[MAX << 1];
int tot = 1, lst = 1;
/*SAM组件*/
void add(int c)
{
	int p = lst;
	int np = lst = ++tot;
	T[np].len = T[p].len + 1;
	while (p && T[p].ch[c] == 0)
	{
		T[p].ch[c] = np;
		p = T[p].fa;
	}
	if (p == 0)
	{
		T[np].fa = 1;
	}
	else
	{
		int q = T[p].ch[c];
		if (T[q].len == T[p].len + 1)
		{
			T[np].fa = q;
		}
		else
		{
			int nq = ++tot;
			T[nq] = T[q];
			T[nq].len = T[p].len + 1;
			T[q].fa = T[np].fa = nq;
			while (p && T[p].ch[c] == q)
			{
				T[p].ch[c] = nq;
				p = T[p].fa;
			}
		}
	}
}
string s;
string t;
int ans = 0;
int maxl[MAX];
int main()
{
	cin >> s >> t;
	int len = s.length();
	s = ' ' + s;
	for (int i = 1; i <= len; i++)
	{
		add(s[i] - 'a');
	}
	len = t.length();
	t = ' ' + t;
	int p = 1;//p 当前所在结点
	int cur = 0;// cur 当前匹配长度
	for (int i = 1; i <= len; i++)
	{
		int v = t[i] - 'a';
		if (T[p].ch[v])//能转移则转移
		{
			cur++;
			p = T[p].ch[v];
		}
		else
		{
			while (p && !T[p].ch[v])//不能转移先跳 fa
			{
				p = T[p].fa;
			}
			if (!p)//倘若跳到头了都不能转移
			{
				cur = 0;
				p = 1;//则重置之
			}
			else
			{
				cur = T[p].len + 1;//否则转移
				p = T[p].ch[v];//注意更新顺序
			}
		}
        maxl[i]=cur;
		ans = max(ans, maxl);
	}
	cout << ans << endl;
}
获取多串的最长公共子串

首先，我们有一个非常暴力的想法，对除了第一个串以外的所有串建 SAM ， 再把第一个串当作 匹配串 ，放到这些 SAM 上去跑，一个字符处理完后，对 $maxl$ 取 $\min$ ，最后取 $maxl$ 中的 最大值。

其次，以上是正解。

为什么？

$maxl$ 的定义是匹配串第 $i$ 位往前最长匹配到了多长。

这个氡氡显然 只与 匹配串，也就是第一个串有关。那么，在每一次跑之间，它们跑出来的信息是可以 叠加 的。

那么我们多次取 $\min$ ，也是被允许的 QaQ 。

板子题一： LCS2 - Longest Common Substring II

板，以下是瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include <bits/stdc++.h>
using namespace std;
const int MAX = 2e5 + 7;
struct node
{
	int len, fa;
	int ch[26];
	int siz;
	node()
	{
		siz = len = fa = 0;
		memset(ch, 0, sizeof(ch));
	}
} T[MAX];
int tot = 1;
int lst = 1;

/*SAM组件*/
void add(int c)
{
	int p = lst;
	int np = lst = ++tot;
	T[np].len = T[p].len + 1;
	T[np].siz = 1;
	while (p && T[p].ch[c] == 0)
	{
		T[p].ch[c] = np;
		p = T[p].fa;
	}
	if (!p)
	{
		T[np].fa = 1;
	}
	else
	{
		int q = T[p].ch[c];
		if (T[q].len == T[p].len + 1)
		{
			T[np].fa = q;
		}
		else
		{
			int nq = ++tot;
			T[nq] = T[q];
			T[nq].siz = 0;
			T[nq].len = T[p].len + 1;
			T[q].fa = T[np].fa = nq;
			while (p && T[p].ch[c] == q)
			{
				T[p].ch[c] = nq;
				p = T[p].fa;
			}
		}
	}
}

string t;//第一个串，即匹配串
char s[MAX];//因为不得不用scanf输入所以被迫用char*
int maxl[MAX];//t[i]向前最长匹配到多长

/*多次建SAM，需要初始化*/
void init()
{
	for (int i = 1; i <= tot; i++)
	{
		T[i] = node();
	}
	tot = lst = 1;
}

int main()
{
	cin >> t;
	int kk = t.length();
	t = ' ' + t;
    
	memset(maxl, 63, sizeof(maxl));//赋极大值
    
	while (scanf("%s", s + 1) != -1)//它不说有多少个串就很烦
	{
		init();
        
		int len = strlen(s + 1);
		for (int i = 1; i <= len; i++)
		{
			add(s[i] - 'a');//建SAM
		}
        
        /*跳SAM，跑匹配*/
		int p = 1;
		int cur = 0;
		for (int i = 1; i <= kk; i++)
		{
			int v = T[p].ch[t[i] - 'a'];
			if (v)
			{
				p = v;
				cur++;
			}
			else
			{
				while (p && !T[p].ch[t[i] - 'a'])
				{
					p = T[p].fa;
				}
				if (p == 0)
				{
					p = 1;
					cur = 0;
				}
				else
				{
					cur = T[p].len + 1;
					p = T[p].ch[t[i] - 'a'];
				}
			}
			maxl[i] = min(maxl[i], cur);//对maxl[i]取min
		}
	}
	int ans = 0;
	for (int i = 1; i <= kk; i++)
	{
		ans = max(ans, maxl[i]);//取maxl中最大的
	}
	cout << ans << endl;
}

板子题二：[SDOI2008]Sandy的卡片

对 差分数组 做多串匹配就好力。

求第 $k$ 大子串

在之前的应用中，您一定已经熟练运用 SAM 暴切各种子串计数题了。（

而求第 $k$ 大子串正是基于子串统计，您必然又能切个爽。

这一大类问题又细分成两小类：本质不同和位置不同。

我们逐一阐述。

本质不同 要求我们忽略 出现位置 的差异进行计数，对于每一位字符，根据字典序判定大小。

首先，我们需要根据SAM上 $ch$ 的转移，构建出一张 DAG 。再以 $1$ 号结点（代表空串的结点）为根，取一棵 26叉生成树 （严谨来说不是，但这样感性理解就够了）。

然后，我们要在这个树上瞎jb跳。

具体地，当我们到达了某个点，我们从 $a$～$z$ 枚举出边，若该子树所包含的子串数 小于 $k$ ，则跳过，当前 $k$ 减去该子树内子串的个数，决策下一条出边。

直到找到第一条出边，其去向子树的 $size$ 大于等于 了当前的 $k$ ，则跳向该子树，相当于当前位选择了 这条出边指向的字符 ，进入下一位的决策……

讲得不明不白，建议作者多学点语文再来这里说话。

如果是不懂思想可以左转 《紫题算法学习实况》 $fhq-treap$ 实现查询第 $k$ 大部分（无端推销）。

建议直接看这部分的瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void dfs(int u, int k)
{
	k--;//先减去自己
	if (k == 0)//若为0说明这就是第k大
		return;
	for (int i = 0; i < 26; i++)//枚举出边
	{
		if (T[u].ch[i])
		{
			if (dp[T[u].ch[i]] < k)//若小于则跳过
			{
				k -= dp[T[u].ch[i]];//减去这些子串
			}
			else
			{
				cout << (char)('a' + i);//该位选择了这个字符
				dfs(T[u].ch[i], k);//进入下一位的决策
				return;
			}
		}
	}
}

我们注意到瑇码里有个 $dp$ 数组，他是干甚么的？根据注释可知，这代表某个 子树内子串 的数量。

但如何求 $dp$ 呢？我们用树形 $dp$ 来搞。

这就是赤裸裸的 子树和 问题，那么这个 $\orange{\texttt{普及-}}$ 树形dp就没有手也行了：

下面是瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int dp[MAX];
void DP(int u)
{
	if (dp[u])
	{
		return;
	}
	dp[u] = 1;
	for (int i = 0; i < 26; i++)//遍历儿子
	{
		if (T[u].ch[i])
		{
			DP(T[u].ch[i]);
			dp[u] += dp[T[u].ch[i]];
		}
	}
}

行百里者半九十，我们乘胜追击，把 位置不同 一起淦掉。

仔细观察前几题的瑇码会发现，笔者像背板似的在 SAM 还维护了一个东西：

T[].siz

它是来干嘛的？

我们先认真撕♂尻这样一个问题，我们在SAM里加点，加哪些点的时候会有新串产生，加哪些点的时候不会呢？

加 $np$ 的时候一定是会产生新串的，这点根据定义就可知， $np$ 本身就是我们在原串后 新加字符 时的产物。

加 $nq$ 的时候呢？我们其实没有新字符吞进自动姬，只是自动姬自己内部的结点 裂开来 而已，串还是那些串，不过是分到了两个等价类罢了/kk 。

所以我们说加 $np$ 会产生新串，加 $nq$ 不会。

那么这个 T[].siz 其实就是某个点 对子串数的贡献 。我们对 T[np].siz 初始化为 $1$ ， 对 T[nq].siz 初始化为 $0$ 。

_需要注意的是 siz 不等于某结点代表的子串数，它是一种贡献，可以看作是一种 差分标记（或许可以这么理解？）_

再放送SAM加字符瑇码，加深印象（水字数）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void add(int c)
{
	......
	int np = lst = ++tot;
	T[np].siz = 1;//mark
	......
	else
	{
		.......
		else
		{
			int nq = ++tot;
			T[nq] = T[q];
			T[nq].siz = 0;//mark
			......
		}
	}
}

这时我们再跑树形 dp ，就得换一个转移方程了。

我们需要先把每个结点 对应的子串数 获取出来，我们说 $siz$ 相当于 差分标记 其实是有原因的，见下qwq：（ $dp2$ 代表某结点（等价类）中的 子串数 ）

然后再跑常规的路径统计：

好吧依然是没有手也行。

板子题一：SP7258 SUBLEX - Lexicographical Substring Search

只要求本质不同，连 siz 都不用写。

瑇码详见后面。

板子题二：[TJOI2015]弦论

抓～紧～时～间～打～板～子～

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1e6 + 7;

/*SAM组件*/
struct node
{
	int len, fa;
	int siz;
	int ch[26];
	node()
	{
		len = fa = 0;
		memset(ch, 0, sizeof(ch));
	}
} T[MAX];
struct SAM
{
	int tot = 1, lst = 1;
	void add(int c)
	{
		int p = lst;
		int np = lst = ++tot;
		T[np].siz = 1;//mark
		T[np].len = T[p].len + 1;
		while (p && !T[p].ch[c])
		{
			T[p].ch[c] = np;
			p = T[p].fa;
		}
		if (!p)
		{
			T[np].fa = 1;
		}
		else
		{
			int q = T[p].ch[c];
			if (T[q].len == T[p].len + 1)
			{
				T[np].fa = q;
			}
			else
			{
				int nq = ++tot;
				T[nq] = T[q];
				T[nq].siz = 0;//mark
				T[nq].len = T[p].len + 1;
				T[q].fa = T[np].fa = nq;
				while (p && T[p].ch[c] == q)
				{
					T[p].ch[c] = nq;
					p = T[p].fa;
				}
			}
		}
	}
} Tree;

int kk = 0;
namespace st1//本质不同
{
	int dp[MAX];
	inline void DP(int u)//树形dp，求子树和
	{
		if (dp[u])
		{
			return;
		}
		dp[u] = 1;
		for (register int i = 0; i < 26; i++)
		{
			if (T[u].ch[i])
			{
				DP(T[u].ch[i]);
				dp[u] += dp[T[u].ch[i]];
			}
		}
	}
	inline void dfs1(int u, int k)//求第k大
	{
		k--;
		if (k == 0)
		{
			return;
		}
		for (register int i = 0; i < 26; i++)
		{
			if (T[u].ch[i])
			{

				if (dp[T[u].ch[i]] < k)
				{
					k -= dp[T[u].ch[i]];
				}
				else
				{
					cout << (char)('a' + i);
					kk = 1;
					dfs1(T[u].ch[i], k);
					return;
				}
			}
		}
	}
	void MAIN()
	{
		DP(1);
		int k;
		cin >> k;
		dfs1(1, k + 1);//是k+1，因为这会被空串消耗一次
	}
} // namespace st1
namespace st2
{
	int dp2[MAX];
	struct edge
	{
		int next, to;
	} e[MAX << 1];
	int head[MAX], eid = 1;
	inline void adde(int x, int y)
	{
		e[++eid].next = head[x];
		e[eid].to = y;
		head[x] = eid;
	}
	inline void DP2(int u)//树形dp，求每个结点对应子串数
	{
		dp2[u] = T[u].siz;
		for (register int i = head[u]; i; i = e[i].next)
		{
			int v = e[i].to;
			DP2(v);
			dp2[u] += dp2[v];
		}
	}

	int f[MAX];
	inline void redfs(int u)//再次树形dp，求子树和
	{
		f[u] = dp2[u];
		for (register int i = 0; i < 26; i++)
		{
			if (T[u].ch[i])
			{
				if (!f[T[u].ch[i]])
				{
					redfs(T[u].ch[i]);
				}
				f[u] += f[T[u].ch[i]];
			}
		}
	}
	inline void dfs2(int u, int k)//求第k大
	{
		k -= dp2[u];//注意：这里被消耗的是 dp2[u] 这么多
		if (k <= 0)
		{
			return;
		}
		for (register int i = 0; i < 26; i++)
		{
			if (T[u].ch[i])
			{
				if (f[T[u].ch[i]] < k)
				{
					k -= f[T[u].ch[i]];
				}
				else
				{
					cout << (char)('a' + i);
					dfs2(T[u].ch[i], k);
					return;
				}
			}
		}
	}
	void MAIN()
	{
		for (register int i = 2; i <= Tree.tot; i++)
		{
			adde(T[i].fa, i);
		}
		DP2(1);
		dp2[1] = 0;
		int k;
		cin >> k;
		redfs(1);
		if (k > f[1])
		{
			cout << -1;
			return;
		}
		dfs2(1, k);
	}
} // namespace st2
char s[MAX];
signed main()
{
	ios::sync_with_stdio(0);
	cin >> s + 1;
	int len = strlen(s + 1);
	for (register int i = 1; i <= len; i++)
	{
		Tree.add(s[i] - 'a');
	}
	int opt;
	cin >> opt;
	if (opt)
	{
		st2::MAIN();
	}
	else
	{
		st1::MAIN();
	}
}

说句闲话：或许 “本质不同” 其实就是 “位置不同” 的 dp2=1 的特殊情况罢……

获取循环同构的出现情况

首先你需要知道甚么是循环同构，我们把一个字符串 $t$ 的 第一个字符放到最后 ，就形成了一个新串，如此往复，它一共会形成 $t.length$ 个新串。

我们把这些新串拿去在另一个串上匹配，看看能匹配上多少。

深得暴力要义的神仙一定已经准备打好多串匹配的代码了，但是除非你是松怪，否则出题人不可能不卡掉你。

我们需要 深入了解 后缀自动姬的工作机理。

我们知道跳 $fa$ 相当于在前面删字符，跳 $ch$ 相当于在后面加字符，所以……

我知道了，但你出言不逊是 ，我们只需要玩 转 后缀自动姬的精妙结构即可，具体步骤如下：

_设匹配串原长为 $n$_

  1. 先对被匹配的串建一只 SAM

  2. 读入匹配串，用 子串判定 类似的方法，能转移则转移，不能转移就跳 $fa$ ，不断在SAM上跳结点。

  3. 把整个串都跳完以后，看看当前跳到的结点的 $len$ 是否 等于 $n$ 。若等于，则说明这是一种在原串中出现过的串，统计进贡献。

  4. 着手在末尾添加字符。照样是能转移则转移，不能转移就跳 $fa$ 。

  5. 着手删去第一个字符。如果 $n-1$ 小于 了该结点的最大长度 $len$ ，$\mathbf{dark}$ 力跳 $fa$ ，否则啥也不干。

  6. 看看当前跳到的结点的 $len$ 是否 等于 $n$ 。若等于，则说明这是一种在原串中出现过的串，统计进贡献。

  7. 如此往复 4.5.6 三步，进行 $n-1$ 遍即可。

板子题： CF235C Cyclical Quest

太 板 了，具体实现看瑇码+注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167

#include <bits/stdc++.h>
using namespace std;
const int MAX = 2e6 + 7;

/*SAM组件*/
struct node
{
	int len, fa;
	int ch[26];
	int siz;
	node()
	{
		siz = len = fa = 0;
		memset(ch, 0, sizeof(ch));
	}
} T[MAX];
int tot = 1;
int lst = 1;
struct edge
{
	int next, to;
} e[MAX << 1];
int head[MAX], eid = 1;
inline void adde(int x, int y)
{
	e[++eid].next = head[x];
	e[eid].to = y;
	head[x] = eid;
}
inline void add(int c)
{
	int p = lst;
	int np = lst = ++tot;
	T[np].len = T[p].len + 1;
	T[np].siz = 1;
	while (p && T[p].ch[c] == 0)
	{
		T[p].ch[c] = np;
		p = T[p].fa;
	}
	if (!p)
	{
		T[np].fa = 1;
	}
	else
	{
		int q = T[p].ch[c];
		if (T[q].len == T[p].len + 1)
		{
			T[np].fa = q;
		}
		else
		{
			int nq = ++tot;
			T[nq] = T[q];
			T[nq].siz = 0;
			T[nq].len = T[p].len + 1;
			T[q].fa = T[np].fa = nq;
			while (p && T[p].ch[c] == q)
			{
				T[p].ch[c] = nq;
				p = T[p].fa;
			}
		}
	}
}

/*dfs处理各个等价类的出现次数*/
int vis[MAX], dp[MAX];
inline void dfs(int u)
{
	dp[u] = T[u].siz;
	for (register int i = head[u]; i; i = e[i].next)
	{
		int v = e[i].to;
		dfs(v);
		dp[u] += dp[v];
	}
}


inline void init()
{
	memset(vis, 0, sizeof(vis));
}
int main()
{
	string t;
	cin >> t;
	int CC;
	cin >> CC;
	int kk = t.length();
	t = ' ' + t;
	for (register int i = 1; i <= kk; i++)
	{
		add(t[i] - 'a');//增量法
	}
	for (register int i = 2; i <= tot; i++)
	{
		adde(T[i].fa, i);//连边
	}
	dfs(1);
    
    
	for (int C = 1; C <= CC; C++)
	{
		int ans = 0;
		string s;
		cin >> s;
		int len = s.length();
		s = ' ' + s;
		int p = 1, cur = 0;
		for (register int i = 1; i <= len; i++)//先跳匹配串，对应步骤2
		{
			while (p && T[p].ch[s[i] - 'a'] == 0)
			{
				p = T[p].fa;
				cur = T[p].len;
			}
            
			if (T[p].ch[s[i] - 'a'])
			{
				cur++;
				p = T[p].ch[s[i] - 'a'];
			}
		}
        
		if (cur == len)//统计，对应步骤3
		{
			if (vis[p] < C)
			{
				ans += dp[p];
				vis[p] = C;//打标记，以防重复统计
			}
		}
        
		for (register int i = 1; i <= len - 1; i++)
		{
			while (p && T[p].ch[s[i] - 'a'] == 0)//末尾添加字符，对应步骤4
			{
				p = T[p].fa;
				cur = T[p].len;
			}
			if (T[p].ch[s[i] - 'a'])
			{
				cur++;
				p = T[p].ch[s[i] - 'a'];
			}

			if (cur > len && --cur == T[T[p].fa].len)//前面删字符，对应步骤5
			{
				p = T[p].fa;
			}

			if (cur == len)//统计，对应步骤6
			{
				if (vis[p] < C)//为防止清空标记太耗时，故看标记的标号，以辨别不同的询问
				{
					ans += dp[p];
					vis[p] = C;
				}
			}
		}
		cout << ans << endl;
	}
}
广义 SAM

不会，不懂，不想写。（鸽子三连）

$\text{LCT}$ （动态树）

“一杯茶，一包烟，一棵LCT调亿天。”

这是神马东东？

一种维护树上信息的 灵活 的数据结构。（灵活，指在网上看到无数种不同的写法），其最大的特点在于能够 动态加边断边 。

您会在接下来很多地方见识到所谓“灵活”的一面。

原理？

把序列上问题强行上树可以变成 毒瘤 ，相反地，把树上问题剖到序列上就会变得清新。

于是 树链剖分 横空出世，其下有重剖、长剖、虚实链剖分三类。

重剖和长剖比较守序，它们都是按树形态的 某一特征 去剖分。

到了虚实链剖分就开始放飞自我了，怎么剖分是随着人为的操作去决定的。作为一个 灵活 的数据结构， $\text{LCT}$ 选择的就是虚实链剖分。

树剖需要一个珂爱的DS来帮助维护剖出的一条一条 链信息 ，因为我们有加边删边， 相对静态 的线段树就显得朝不保夕。我们把目光投向了平衡树。

在那么多平衡树里， $splay$ 受到了人类的青睐，它对结点的 添加、删除、移动 可以说是行云流水，流畅异常。

所以我们选中 $splay$ 作为辅助维护链信息的DS（后文称之为辅助树），而这里的 $splay$ ，瑇码更近似于《文艺平衡树》。

_闲话：其实 fhq-treap 也能做 qwq ，只是多了个 log 罢了_

实现？

接下来，我们尝试用这个 “灵活” 的 LCT ，来实现加边、删边、路径加、路径乘、路径求和。

为了装腔作势借以吓人， 我们列举一下一棵 LCT 需要打的珂怕的函数们：

  • 正统 $splay$ 系：$iden$，$push_up$，$push_down$

  • $splay\;\times\;LCT$ 混血 （趋近LCT国情的 $splay$ 写法改造）：$isroot$，$rotate$，$splay$

  • $LCT$ 本地居民：$access$，$make_root$，$split$，$find$，$link$，$cut$

作者意识到自己LCT只会背板子，得找时间深♂入重学

回滚莫队

果然还是小清新数据结构适合我。

这是神马氡氡

如果我有一个区间询问，是 $\mathcal{O}(1)$ 插入， $\mathcal{O}(inf)$ 删除的。

普通的莫队在这里就GG了，因为他不可避免地要删除。

此时回滚莫队横空出世。

这是一种能有效鸽掉 插入/删除 之间任意一种操作的高级膜队技巧。

思想？？？

删除不能，那我还不能暴力呗。

这是一个臭数组，已经被野兽先辈偷偷用 $sqrt(n)$ 分好了块：

假设我们求 $[3,5]$ 的区间众数，这玩意加入新元素很轻松，但是删除元素就有些危机。

从 $L$ 到 $R$ ，这是 $L$ （3），这是 $R$ （5）。这些边我不加，这些边我不加！

暴力怎么做？暴力是不是？装桶，装桶，装桶，然后 $for$ 循环查询。

这个是要用的，先打好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int c[MAX];
int baoli(int l, int r)
{
	int ans = 0;
	for (int i = l; i <= r; i++)
	{
		c[num[i]]++;//装桶装桶
	}
	for (int i = l; i <= r; i++)
	{
		if (c[num[i]] > c[ans])//for循环查询
		{
			ans = num[i];
		}
	}
	for (int i = l; i <= r; i++)//珍爱生命，远离memset
	{
		c[num[i]]--;
	}
	return ans;
}

这个暴力看上去十分 naive ，接下来，回滚莫队将会展现块与块之间的信息交流的真正妙处。

对于这个 $[3,5]$ 的区间查询，我们先把两个指针，都拉到 $3$ 所在这个块的右边，夹出一块 空区间。

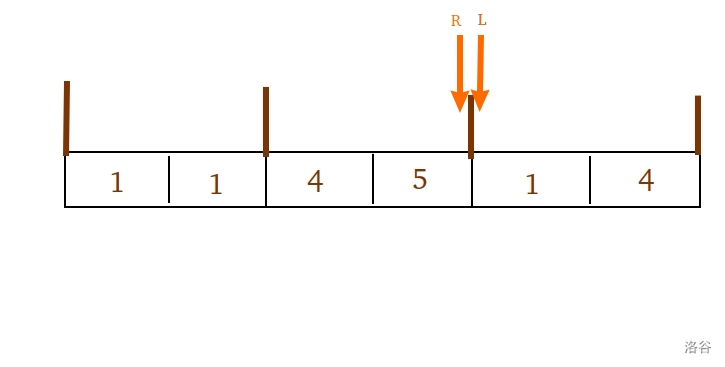
_注：L指针永远指向一格的左边，R指针永远指向一格的右边，以此表示[L,R]是闭的。_

首先我们优先移动 $R$ 指针，它会不断移移移，一路上 add(++R) 。

当我们把 $R$ 移到 $5$ 的时候，我们先 在这停顿 ，记录下此时更新到的 众数 $maxx$ ，开一个变量 $store=maxx$ ，显然 $store=1$ 。

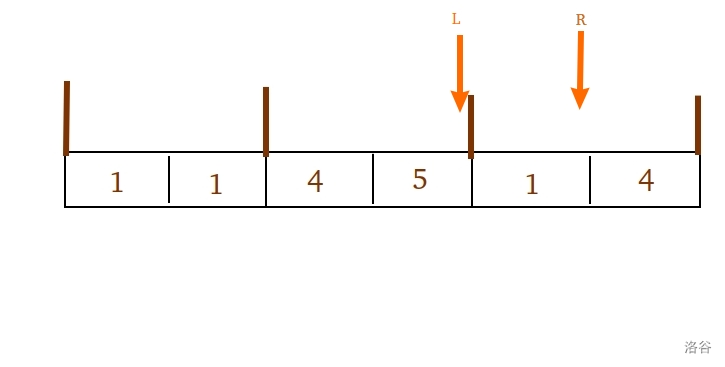
这时，我们再向左移动 $L$ 指针，它会不断移移移，一路上 add(--L) 。

等我们移到 $3$ 的时候，我们获得了对于该询问的答案，记录之。

这时我们要询问 $[4,5]$ 了，但我们意识到一个很严肃的问题：如果删了众数，我们的程序无法知道他的继承人是谁。

我们之前不是保存了一个 $store$ 表示上图当时情况下的 $maxx$ 吗，我们选择在回答完 $[3,5]$ 后 恢复 $L$ 指针到 块右边界 。

由此一来，两个指针又形成了上图的形势，我们又可以重新任用我们的 $store$ 作为 $maxx$ 了。

以下是处理询问部分的瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*tot——当前处理的询问排序后的编号 ，i——该询问左端点所在块 */
while (R < q[tot].r)//移右指针
{
	add(++R);
}
int store = maxx;//在这停顿

while (L > q[tot].l)//移左指针
{
	add(--L);
}
COUT[q[tot].id] = maxx;//保存答案

maxx = store;//重新任用store作为maxx
while (L <= rm[i])//恢复现场
{
	cnt[num[L++]]--;//把被加上的cnt减回来
}

您可能会感到困惑，为什么又有一个 $tot$ ，又有一个 $i$ 。我们到底在枚举什么？

其实理解了上述思想就自证不难了，我们每次需要把 $L$ 指针移到块右边界，又因膜队的精髓在于尽可能鸽掉 端点的移动 ，所以我们必然是枚举 块（i） 更河里，而 $tot$ 只是顺带着枚举一枚举。

但是还有一个问题，我们每次是把 $R$ 端点右移，我们不能左移 $R$ ，因为左移意味着 删除 ，而 $R$ 一开始又是在块的右边界上，也就默认了这个询问必然会 跨块 ，那不跨块的询问怎么办？

别忘了我们的暴力怎么做。不跨块询问区间内元素是 $\sqrt{N}$ 级别的，自然可以放心大胆地暴力。

所以核心瑇码就是这样的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int L = 1, R = 0;
int tot = 1;
for (int i = 1; i <= B; i++)//B是块数，这里是枚举块
{
	memset(cnt, 0, sizeof(cnt));
	maxx = 0;//归零面对新块
    
	R = rm[i];//R指针放在右边界
	while (block[q[tot].l] == i)//对于所有左端点在这个块里的
	{
		L = rm[i] + 1;//左端点移到右边界+1，以表空区间
		if (q[tot].r - q[tot].l <= M)//小于根号，暴力好耶
		{
			COUT[q[tot].id] = baoli(q[tot].l, q[tot].r);
		}
		else//不再重复
		{
			while (R < q[tot].r)
			{
				add(++R);
			}
			int store = maxx;
			while (L > q[tot].l)
			{
				add(--L);
			}
			COUT[q[tot].id] = maxx;
			maxx = store;
			while (L <= rm[i])
			{
				cnt[num[L++]]--;
			}
		}
		tot++;
	}
}

如果您 naive 地随手上了一个奇偶排序优化，那么之前的努力全部木大。

因为右端点只许右移，所以排序时同块的询问只能以 右端点递增 排序。

我们甚至可以用回滚莫队水掉大部分普通莫队的题，复杂度也没差，几乎就是上位了。（当然询问的东西太大（比如一个栈），不能低复杂度保存和重新启用时，还是只能普通莫队）

劲爆例题：

板子题：歴史の研究

比【模板】还模板的模板题。

要求的是 $\max\{num[i]\cdot cnt[num[i]]\}$ 。

这个东西好增不好删，我们着手使用只增不删回滚莫队。

$\text{add}$ 时不断更新 $maxx$ ，回答完一个询问就直接洗地。

存在一个注意点是，这题需要离散化，而上面公式里的第一个 $num[i]$ 应是 离散化前 的原值。（可能只有我这种弱智才会因为这个犯错）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include <bits/stdc++.h>
using namespace std;
const int MAX = 2e5 + 7;
#define int long long
struct query
{
	int l, r, id;
} q[MAX];
int block[MAX];
bool cmp(query a, query b)
{
	if (block[a.l] != block[b.l])
	{
		return a.l < b.l;
	}
	return a.r < b.r;
}
int N, Q;
int M, B;
int cnt[MAX];
int num[MAX];
int tmp[MAX];
int sum = 0;
void lsh()
{
	memcpy(tmp, num, sizeof(num));
	sort(tmp + 1, tmp + 1 + N);
	for (int i = 1; i <= N; i++)
	{
		num[i] = lower_bound(tmp + 1, tmp + 1 + N, num[i]) - tmp;
	}
}

void add(int p)
{
	cnt[num[p]]++;
	sum = max(sum, tmp[num[p]] * cnt[num[p]]);
    //因为原数组被复制到了tmp数组里去，num[p]其实是其下标
    //所以tmp[num[p]]就是原值了
}
int c[MAX];
int baoli(int l, int r)
{
	int kel = 0;
	for (int i = l; i <= r; i++)
	{
		c[num[i]]++;
	}
	for (int i = l; i <= r; i++)
	{
		kel = max(kel, c[num[i]] * tmp[num[i]]);
	}
	for (int i = l; i <= r; i++)
	{
		c[num[i]]--;
	}
	return kel;
}
int lm[MAX], rm[MAX];
void pre()
{
	B = N / M;
	for (int i = 1; i <= B; i++)
	{
		lm[i] = rm[i - 1] + 1;
		rm[i] = lm[i] + M - 1;
	}
	if (N % M)
	{
		B++;
		lm[B] = rm[B - 1] + 1;
		rm[B] = N;
	}
}

int COUT[MAX];
signed main()
{
	cin >> N >> Q;
	M = sqrt(N);
	for (int i = 1; i <= N; i++)
	{
		cin >> num[i];
		block[i] = (i - 1) / M + 1;
	}
	for (int i = 1; i <= Q; i++)
	{
		cin >> q[i].l >> q[i].r;
		q[i].id = i;
	}
	sort(q + 1, q + 1 + Q, cmp);
	pre();
	lsh();//离散化
    
    /*回滚莫队板子*/
	int L = 1, R = 0;
	int tot = 1;
	for (int i = 1; i <= B; i++)
	{
		memset(cnt, 0, sizeof(cnt));
		sum = 0;
		R = rm[i];
		while (block[q[tot].l] == i)
		{
			L = rm[i] + 1;
			if (q[tot].r - q[tot].l <= M)
			{
				COUT[q[tot].id] = baoli(q[tot].l, q[tot].r);
			}
			else
			{
				while (q[tot].r > R)
				{
					add(++R);
				}
				int store = sum;
				while (q[tot].l < L)
				{
					add(--L);
				}
				COUT[q[tot].id] = sum;
				sum = store;
				while (L <= rm[i])
				{
					cnt[num[L++]]--;
				}
			}
			tot++;
		}
	}
	for (int i = 1; i <= Q; i++)
	{
		cout << COUT[i] << endl;
	}
}

板子题二：【模板】回滚莫队&不删除莫队

不板的丢人模板题

要求 相距最远的相同数 的距离。

某个数的 极左/极右出现位置 ($fir[i],rig[i]$) 或许很好装，也便于 $\mathcal{O}(1)$ 更新， $\mathcal{O}(1)$ 算答案（ $rig[i]-fir[i]$ ）。

但是我们洗地会极其低效，何出此言？

因为极左这个 “极” 字意味着我们不是那么容易恢复现场。举个例子：（这个数组里的臭气被稍加稀释）

回答完 $[1,6]$ 这个询问后，我们是把 $L$ 指针恢复到块右边界，一路上把 $fir[num[i]]$ 清空成 $0$ 。

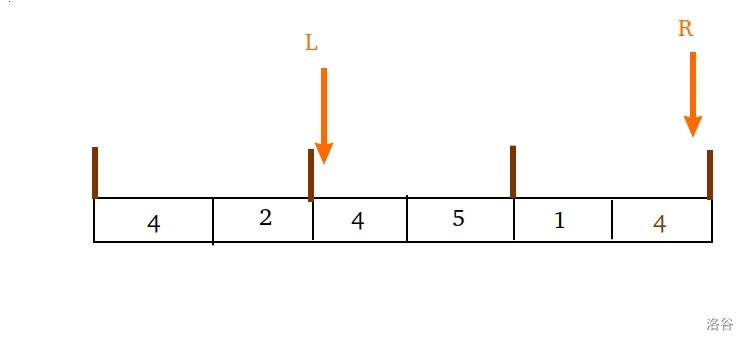
但如果我们把 $fir[4]$ 清空成 $0$ ，这说明它不再出现。可事实上，$4$ 这个数却确确实实存在于 $L$ 和 $R$ 之间。

如果接下来查询的是 $[2,6]$ ，我们就出锅了，因为我们不再知道在 $3$ 号位置上还有一只 $4$ 。

意识到 $fir$ 的能力是有极限（右边界）的， 维护的数的位置 越是在 左端点所在块 外，清空效力就越鞭长莫及。

所以，我不维护啦，JOJO！

这里就分出三种情况来：

  • 对于所有相同数都在块内的情况，我们 $fir$ 是可以顺利完成清空的（从左往右扫，最终清空全块）。

  • 对于一个相同数在块内，一个相同数在块外的情况，即使不小心误清空也不会出锅。反正这个数也只剩一只了，而题目要求的是相距最远的 两个，本就统计不进答案。

  • 但有时会出现 两个相同数都在块外 的情况，所以我们需要对这种情况进行异化处理。

我们改变 极左位置（ $fir$ ） 的定义是：在 该块右边界之后 的极左位置。这样我们就可以对两个相同数 都在块外 的情况进行 块内清空后 的查询。

然而我们不能大E，这样的话，拿什么去算 两个相同数都在块内 的答案呢？

我们致远星地发现在同一次查询中，传入 $\text{add}$ 的 $L$ 永远 递减 ，也就是说，其实我们每次传进去的 $L$ 就已经是这个位置上的数的 极左位置 了。

那么也不需要开新数组，以下是 $\text{add}$ 的瑇码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void add(int p, int opt)//opt——若这次移的是L则为1，反之为2
{
	if (opt == 1)
	{
		if (rig[num[p]] == 0)
        //即使我是一个在块内的数
        //但当块外没有相同数的时候，我就是极右的位置
		{
			rig[num[p]] = p;
		}
		maxx = max(maxx, rig[num[p]] - p);//直接用 p 就好了
	}
	if (opt == 2)
	{
		if (fir[num[p]] == 0)
        //因为 R 永远递增
        //所以如果没有块外极左数，那么这个就是了
		{
			fir[num[p]] = p;
			dq.push_back(p);
       		//dq 存一些需要清空 fir 的位置
            //到时候对 dq 里的元素一一清空就是
		}
		rig[num[p]] = p;//同上的理由，直接用 p 就好了
		maxx = max(maxx, rig[num[p]] - fir[num[p]]);
	}
}

很好很好，那么该什么时候清空呢？我们奉行一条原则：

『块内信息在 单次询问结束 后清空，块外信息在 块内所有询问结束 后清空』

首先，对于 $fir$ 数组不用急着清空，因为这是右边界往后，块外的事了。

其次，对于不在块内的 $rig[i]$ 不用急着清空，原因同上。

换言之，我们只需在一次询问后清空在 块内 的 $rig$ 们就可以了。

等到这一块的询问们都已经完成，我们就可以清空 $fir$ 和 $rig$ ，具体要清空的位置已经装到 $dq$ 里了。之所以要存起来再清空，是因为 memset/no。

全瑇码装填：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
#include <bits/stdc++.h>
using namespace std;
const int MAX = 4e5 + 7;

/*莫队组件*/
struct query
{
	int l, r;
	int id;
} q[MAX];
int block[MAX];
bool cmp(query a, query b)
{
	if (block[a.l] != block[b.l])
	{
		return a.l < b.l;
	}
	if (a.r != b.r)
		return a.r < b.r;
	return a.l < b.l;
}
int N, Q;
int lm[MAX], rm[MAX];
int B, M;
void pre()
{
	M = sqrt(N);
	B = N / M;
	for (int i = 1; i <= N; i++)
	{
		block[i] = (i - 1) / M + 1;
	}
	for (int i = 1; i <= B; i++)
	{
		lm[i] = rm[i - 1] + 1;
		rm[i] = lm[i] + M - 1;
	}
	if (N % M)
	{
		B++;
		lm[B] = rm[B - 1] + 1;
		rm[B] = N;
	}
}

/*离散化*/
int tmp[MAX];
int num[MAX];
void lsh()
{
	memcpy(tmp, num, sizeof(num));
	sort(tmp + 1, tmp + 1 + N);
	for (int i = 1; i <= N; i++)
	{
		num[i] = lower_bound(tmp + 1, tmp + 1 + N, num[i]) - tmp;
	}
}

/*add*/
int fir[MAX], rig[MAX];
vector<int> dq;
int maxx = 0;
void add(int p, int opt)
{
	if (opt == 1)
	{
		if (rig[num[p]] == 0)
		{
			rig[num[p]] = p;
		}
		maxx = max(maxx, rig[num[p]] - p);
	}
	if (opt == 2)
	{
		if (fir[num[p]] == 0)
		{
			fir[num[p]] = p;
			dq.push_back(p);
		}
		rig[num[p]] = p;
		maxx = max(maxx, rig[num[p]] - fir[num[p]]);
	}
}

/*暴力怎么做？！*/
int ll[MAX], rr[MAX];
int baoli(int l, int r)
{
	int ans = 0;
	for (int i = l; i <= r; i++)
	{
		if (!ll[num[i]])
		{
			ll[num[i]] = i;
		}
		rr[num[i]] = i;
	}
	for (int i = l; i <= r; i++)
	{
		ans = max(ans, rr[num[i]] - ll[num[i]]);
	}
	for (int i = l; i <= r; i++)
	{
		ll[num[i]] = rr[num[i]] = 0;
	}
	return ans;
}
int ans[MAX];
int main()
{
	cin >> N;
	pre();
	for (int i = 1; i <= N; i++)
	{
		cin >> num[i];
	}
	lsh();
	cin >> Q;
	for (int i = 1; i <= Q; i++)
	{
		cin >> q[i].l >> q[i].r;
		q[i].id = i;
	}
	int L = 1, R = 0;
	int tot = 1;
	sort(q + 1, q + 1 + Q, cmp);
	for (int i = 1; i <= B; i++)
	{
		R = rm[i];
		maxx = 0;
		while (block[q[tot].l] == i)
		{
			L = rm[i] + 1;
			if (q[tot].r - q[tot].l <= M)
			{
				ans[q[tot].id] = baoli(q[tot].l, q[tot].r);
			}
			else
			{
				while (R < q[tot].r)
				{
					add(++R, 2);
				}
				int store = maxx;
				while (L > q[tot].l)
				{
					add(--L, 1);
				}
				ans[q[tot].id] = maxx;
				maxx = store;
				while (L <= rm[i])
				{
					if (rig[num[L]] == L)//清空块内rig
                    //等价于其极右位置在该块右边界之前
					{
						rig[num[L]] = 0;
					}
					L++;
				}
			}
			tot++;
		}
		for (int j = 0; j < dq.size(); j++)//清空fir和块外rig
		{
			rig[num[dq[j]]] = 0;
			fir[num[dq[j]]] = 0;
		}
		dq.clear();
	}
	for (int i = 1; i <= Q; i++)
	{
		cout << ans[i] << '\n';
	}
}

这个板题一点也不板/fn

板子题三：Rmq Problem / mex

让我 DIO 回滚莫队来切这道线段树题。

我们之前说，回滚莫队可以咕掉删除和插入中的任意一种，但是我们还没见到 咕掉插入 的回滚莫队。

那么这道就是了。

我们发现删除操作非常容易，看看新删的数是不是不出现了，如果不出现了是不是可以更新答案了。

但加入操作就面临着和 $\color{purple}{\texttt{給朝}}$ 一样的危机——找不到继承人。

那么加入操作不咕也得咕了。

怎么咕？我们把咕删除的回滚莫队换个皮即可。

先把之前的板子 再 放 送 ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int L = 1, R = 0;
int tot = 1;
for (int i = 1; i <= B; i++)//B是块数，这里是枚举块
{
	memset(cnt, 0, sizeof(cnt));
	maxx = 0;//归零面对新块
    
	R = rm[i];//R指针放在右边界
	while (block[q[tot].l] == i)//对于所有左端点在这个块里的
	{
		L = rm[i] + 1;//左端点移到右边界+1，以表空区间
		if (q[tot].r - q[tot].l <= M)//暴力
		{
			COUT[q[tot].id] = baoli(q[tot].l, q[tot].r);
		}
		else
		{
			while (R < q[tot].r)
			{
				add(++R);
			}
			int store = maxx;
			while (L > q[tot].l)
			{
				add(--L);
			}
			COUT[q[tot].id] = maxx;
			maxx = store;
			while (L <= rm[i])
			{
				cnt[num[L++]]--;
			}
		}
		tot++;
	}
}

可以看出我们咕删除的回滚莫队是从一个 空区间 一步一步加元素来获取到询问区间的，这个过程中只有加没有删。

那么我们咕加入的回滚莫队就是从一个 满区间 一步一步删元素来获取到询问区间的，这个过程中只有删没有加。

看上去就像这样？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
for (int i = 1; i <= B; i++)
{
	mex = kk;//kk是整个数组的mex，这个可以O(n)预处理
	while (R < N) //移动右指针到尽头
	{
		if (num[++R] <= N + 1)//mex答案一定 N+1 以下，这个随便证明
		{
			cnt[num[R]]++;
		}
	}
	while (L < lm[i]) //移动左指针到左边界
	{
		del(L++);
	}
    //这样一来我们框出了一个 [lm[i],N] 的区间
    //可以保证这一块的所有询问一定在这个区间中发生
    
	kk = mex;
	while (block[q[tot].l] == i)//大体相同
	{
		if (block[q[tot].r] == i)//和作差等价的写法，换换口味
		{
			COUT[q[tot].id] = baoli(q[tot].l, q[tot].r);
		}
		else
		{
			while (R > q[tot].r)
			{
				del(R--);
			}
			int store = mex;
			while (L < q[tot].l)
			{
				del(L++);
			}
			COUT[q[tot].id] = mex;
			mex = store;
			while (L > lm[i])
			{
				if (num[--L] <= N + 1)
				{
					cnt[num[L]]++;//恢复L指针到左边界
				}
			}
		}
		tot++;
	}
}

那么这个 $\text{del}$ 函数里面是肾么呢？

正如我们之前说的“康康新删的数是不是不出现了，如果不出现了是不是可以更新答案了”。这个很好写，在此不表。

还有一个问题，这个排序还能按源赖这么排吗？

答案是否定的，因为你的 $R$ 指针将会从右往左递减，所以应在 $L$ 同块时将 $R$ 降序 排列。

那么你就可以把回滚莫队板子改几个bit直接爆切此题了！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
#include <bits/stdc++.h>
using namespace std;
const int MAX = 2e5 + 7;
struct query
{
	int l, r;
	int id;
} q[MAX];
int block[MAX];
bool cmp(query a, query b)
{
	if (block[a.l] != block[b.l])
	{
		return a.l < b.l;
	}
	return a.r > b.r;
}
int N, Q, M, B;
int num[MAX], cnt[MAX];
int mex;
void del(int p)
{
	if (num[p] <= N + 1) //答案上界为N+1，所以只统计到N+1
	{
		cnt[num[p]]--;
		if (cnt[num[p]] == 0) //如果有一个数被删没了
		{
			mex = min(mex, num[p]); //看看这个数能不能作新mex
		}
	}
}
int c[MAX];
int baoli(int l, int r) //暴力，交了一发没锅
{
	int ans = 0;
	for (int i = l; i <= r; i++)
	{
		if (num[i] <= N + 1)
		{
			c[num[i]]++;
			while (c[ans]) //找到下一个没出现的
			{
				ans++;
			}
		}
	}
	for (int i = l; i <= r; i++) //恢复现场
	{
		if (num[i] <= N + 1)
		{
			c[num[i]]--;
		}
	}
	return ans;
}
int lm[MAX], rm[MAX];
void pre() //预处理每块左右界
{
	B = N / M; //块数
	for (int i = 1; i <= B; i++)
	{
		lm[i] = rm[i - 1] + 1;
		rm[i] = lm[i] + M - 1;
	}
	if (N % M) //如果不能整除
	{
		B++; //开一边角块
		lm[B] = rm[B - 1] + 1;
		rm[B] = N;
	}
}
int tmp[MAX];
int COUT[MAX];
int main()
{
	cin >> N >> Q;
	M = sqrt(N);
	for (int i = 1; i <= N; i++)
	{
		cin >> num[i];
		block[i] = (i - 1) / M + 1;
		if (num[i] <= N + 1)
		{
			cnt[num[i]]++; //用于求最初mex
		}
	}
	while (cnt[mex])
	{
		mex++; //得到全局mex
	}
	for (int i = 1; i <= Q; i++)
	{
		cin >> q[i].l >> q[i].r;
		q[i].id = i;
	}
	pre();
	sort(q + 1, q + 1 + Q, cmp);
	int L = 1, R = N;
	int tot = 1;
	int kk = mex;
	for (int i = 1; i <= B; i++)
	{
		mex = kk;
		while (R < N) //移动右指针到尽头
		{
			if (num[++R] <= N + 1)
			{
				cnt[num[R]]++;
			}
		}
		while (L < lm[i]) //移动左指针到
		{
			del(L++);
		}
		kk = mex;

		while (block[q[tot].l] == i)
		{
			if (block[q[tot].r] == i)
			{
				COUT[q[tot].id] = baoli(q[tot].l, q[tot].r);
			}
			else
			{
				while (R > q[tot].r)
				{
					del(R--);
				}
				int store = mex;
				while (L < q[tot].l)
				{
					del(L++);
				}
				COUT[q[tot].id] = mex;
				mex = store;
				while (L > lm[i])
				{
					if (num[--L] <= N + 1)
					{
						cnt[num[L]]++;
					}
				}
			}
			tot++;
		}
	}
	for (int i = 1; i <= Q; i++)
	{
		cout << COUT[i] << endl;
	}
}

Polya 定理

你会发现 qst 这个废物甚至连定理的名字都打不出来，好在问题不是很大。

这是神马东东

Polya 定理是一种通过计算置换群来数出染色方案的一种神仙玩意，当然这只是数学菜鸡的口胡理解，也就图一乐，真要看严谨说法还得看队爷们的论文。

性感理解置换

  • 我们把 $(^{1\ 2\ 3\ 4\ 5\ 6}_{1\ 3\ 2\ 5\ 6\ 4})$ 这样的上面是一个排列，下面是一个排列的东东叫做置换。
  • 可以把他看作是一个加密规则，加密的过程相当于把一个上面的数替换成下面的数。
  • 我们总是能从置换里找到一些循环，比如 $(^{1\ 2\ 3\ 4\ 5\ 6}_{1\ 3\ 2\ 5\ 6\ 4})$ 就由 $(^{1}_{1})(^{2\ 3}_{3\ 2})(^{4\ 5\ 6}_{5\ 6\ 4})$ 三个循环组成。
  • “组成”这个动词显得非常 naive ，我们一般称：这个置换是这些循环的乘积。
  • 不动点，顾名思义，就是经过置换后不变的元素。
  • 对于置换，我们也定义了两个置换的乘积：$P_1=\binom{1\ \ 2\ \ 3\ \ 4}{a_1\ a_2\ a_3\ a_4},P_2=\binom{a_1\ a_2\ a_3\ a_4}{b_1\ b_2\ b_3\ b_4},P_1*P_2=\binom{1\ \ 2\ \ 3\ \ 4}{b_1\ b_2\ b_3\ b_4}$
  • 看上去就像原序列先经过 $P_1$ 加密规则加密后的密文，再用 $P_2$ 加密一遍？
  • 置换群就是一堆置换的集合。

Burnside 引理

事实上直接背诵这个引理的内容就完全够用了，如果要去强行理解那些“稳定化子”啥的概念的话可能一不小心就会掉进群论的深渊（（

有些题目让我们数一些对象的染色方案，这些染色方案会有一个“置换等价”的限制，即：

如果通过某种特定的变换，两组染色方案可以互相转化，则称这两个方案是本质相同的。

Burnside 引理就是用来数这种受“置换等价”限制的玩意的。

你可以在各大网站上看到这个引理名字的无数种翻译，什么“烧边”啊，“伯恩赛德”啊，为了不至于造成差异，这里直接采用英文。

在 Burnside 引理中，我们用 染色方案的置换 来表达变换的动作，那题目给出的这些变换就组成了一个置换群。

设 $G$ 是给出的置换群，$C(f)$ 是置换 $f$ 中不动点的个数，$N(G,C)$ 表示所有本质不同的染色方案种类数。

其内容如下：

用人话翻译一遍，就是：染色方案的数量是 所有置换中不动点个数 的平均数。

现在您可能还是一头雾水，不妨下面我们尝试运用这一武器来数一些东西。

试看看：

有一个 $2\times2$ 的方格，我们可以将每一格染成红色或白色，如果通过旋转一定角度，两组染色方案可以互相转化，则称这两个方案是本质相同的，求本质不同染色方案数。

本质不同波兰国旗计数

我们先把所有染色方案列出来，一共有 $2^4=16$ 种。

题目给出了置换等价的信息是旋转等价，胡乱思尻一下就知道其实只有四种可能的旋转角度（默认顺时针）：0°，90°，180°，270°。

我们把染色方案从1到16标号，用旋转90度作为栗子，我们尝试用置换来表达【旋转90度】这一动作：

X号元素置换到Y号，就代表X号染色方案旋转90°达到Y号方案。（你也大可理解成X号是Y号方案旋转90°得来，只不过要换一种写法，不动点的个数还是一样的qaq）

那么扳手指头就知道这一置换有 2 个不动点。

把所有旋转情况的不动点个数都扳出来后，再套上珂爱的 Burnside 引理求解：

那么本质不同的 波兰国旗 染色方案就有 6 种辣，经过手玩验证 ，这一答案是正确的。

Polya 定理

刚才扳手指头的过程让我们感到苦涩（至少我打 Latex 打得很苦涩），如果我们数的不是波兰国旗而是俄罗斯国旗甚至泰国国旗，那我们的手指恐怕有些危机。

而 Polya 定理的出现挽救 OIer 于水深火热之中（（

Polya 定理并不依赖于求出置换群的过程，也就是说，我们不需要求出染色方案的置换群就可以直接数。

其内容大致如下。

我们之前是用【染色方案的置换】来表达一个动作的，但事实上，这样的数据往往是巨大多量的。

这时我们发现，在旋转过程中，染色对象内部的各个元素也存在一个置换关系，比如这样：

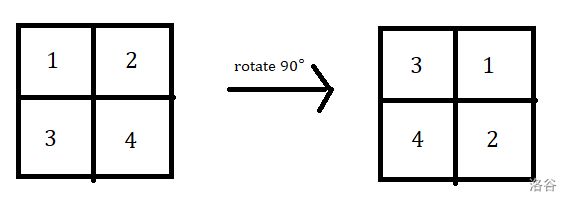
旋转 90° 的变换，其实对象内部存在置换 $\binom{1\ 2\ 3\ 4}{3\ 1\ 4\ 2}$ 。

如果我们不求出各个染色方案之间的置换，而只关注于染色对象内部的元素的置换，就把处理的置换规模从 $M^N$ 级别转化成了 $N$ 。

我们知道一个置换可以拆分成几个循环的乘积，设 $R(f)$ 为置换 $f$ 中的循环个数（这里的置换是 对象内部元素 的置换），$M$ 为颜色数，我们有：

还是一样的题，我们用 Polya 定理来切这道题：

转 90° 会带来对象内元素什么样的置换？之前已经提到了，是 $\binom{1\ 2\ 3\ 4}{3\ 1\ 4\ 2}$ ，这个置换中有 1 个循环。

同理，转 180° 的置换是 $\binom{1\ 2\ 3\ 4}{4\ 3\ 2\ 1}$ ，这个置换中有 2 个循环。

而转 270° 有 1 个循环，转 0° 有 4 个循环。

那么答案就是：

这和我们烧边烧出来的结果是一样的。

好耶！

数波兰国旗非常无聊且枯燥，因为循环节用脚趾头也能数出来，接下来我们尝试数项链。

我们定义一串项链由一圈珠（柱）子串成，它满足旋转同构，即旋转一定角度后相同则本质相同。

咕咕咕！

最后更新： 2021年04月18日 16:33

原始链接： https://quest233.github.io/2021/04/17/%E7%B4%AB%E9%A2%98%E7%AE%97%E6%B3%95%E5%AD%A6%E4%B9%A0%E5%AE%9E%E5%86%B5-II/