因为进不去复赛就只能休养休养生息,整点算法学学。
和同机房的神仙相比,窝挖的坑实在是太多了 $OvO$ 。
2020-10-21:竟然与he老爷讲课撞车了,两相对比显然突出窝的菜
2020-11-16:CSP-S又垫底了,可以安心写博客力
2020-12-26:该文章已停更,光标几乎卡的动不了了
《实况一》(本文)中包含的内容:
点分治
点分树
fhq
网络流
杜教筛
点分治
“每天就是切一些 N 倍经验题,维持维持生活这样子。”
处理什么问题:
大部分是树上点对距离问题,当然还有一些变形。(树论毒瘤爪巴)
如果给您一棵树,让您查询树上是否存在两点距离为 $K$ 。您没学过点分治,您怎么做?
您说,您会暴力 $O(n^2)$ 枚举点对查询其距离!
抱歉,点分治是可以 $O(n\log n)$ 的。
思想是什么:
现在讲一下思想。
树上两点之间,路径唯一 ,两点通向LCA的路径的并,即为两点之间的路径。
这种路径要分类无非两种:过 全树的根 结点的,和 不过根 结点的。
或者换种说法,LCA是全树的根结点的,或者不是根结点的。
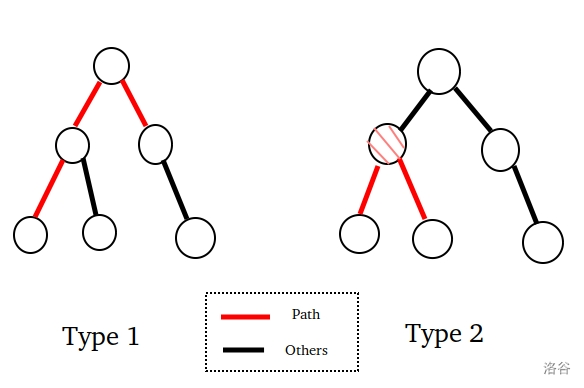
(超喜欢这个字体 $AwA$ )
分类讨论绝对是树学界存在的最恶心的玩意。不会真的有人在代码里分类讨论吧,不会吧不会吧。
我想把这两种情况 归为一类 。
大眼观察法看出 $Type\ 2$ 在以粉色点为根的时候就可以归纳为一种 $Type\ 1$ 。
$Type\ 1$ 多好求,两点到 $LCA$ 距离一加就是了。
显然,我们要从根结点一层一层地递归下去求解。
获得了 $O(level\cdot n)$ ( $level$ 是树的深度)的优秀复杂度!
然后当场就被链卡回了 $O(n^2)$ 。
我们发现,它被卡了,究其原因就是因为树的形态太 $hentai$ 。
一棵树,存不存在距离为 $K$ 的点对,和让谁来当根有关系吗?
没有关系。
那我们就该选一个好亿点的点来当根哇。
这个“好亿点”,具体指的就是,以它来当根,能使 树的深度最小 。
这里有一个概念叫树的重心:
我们知道在一棵树上,删去一个点后,剩下的部分必然不联通。
如果一个点删去它后,剩余的几部分中 大的那一块最小 ,则我们说这个点是这个树的重心。
不难感觉到,如果以一棵树的重心为根,它的佐佑两边会最为“平衡”。
在最美好的愿景下,每层以重心作根可以做到把树二等分。
那二等分又二等分,最终能控制在 $\log n$ 的递归层数。
获得了 $O(n \log n)$ 的优秀复杂度!(大喜)
撒花撒花~
劲爆习题:
模板题:P3806 【模板】点分治1 :(想不到叭,模板就是紫的 $QwQ$ )
给定一棵有 $n$ 个点的树,询问树上距离为 $k$ 的点对是否存在。
裸题,8说了,该说的都在注释里。
1 |
|
次模板题:P4178 Tree
由上题的询问存在与否变成了询问 点对数 ,要求变成了 小于等于 。
点分治的板子该打还是打,但要改一下 $\operatorname{calc}$ 函数。
上一题的策略是:存桶,查能和它拼成 $K$ 的距离是否存在。
但我们这么整是因为题目要求的是等于 $K$ ,所以能拼的距离是唯一确定哒。
可这题是不确定的,所以得换一种思路。
我们尝试把所有出现过的距离排个序,有两个指针 $L$ 和 $R$ 从数组两边往中间逐步压缩。
$L$ 指向的距离和 $R$ 指向的距离,会拼出一种可能的距离。
可以证明这样能不重不漏地拼出树上存在的每一种 两点距离 。
甚至可以在线/fad/fad 。
1 |
|
次次模板题:[国家集训队]聪聪可可
这回求的是距离是 $3$ 的倍数的点对数。照样改 $\operatorname{calc}$ 。
带了亿亿亿亿亿点思维,但是易见平凡(雾。
装桶的思路还是不变,但是开这么多桶贞德合理吗?
两个数 $A,B$ 的 和 $\bmod 3$ 余 $0$ 。则跑不出三种情况:
$A \bmod 3=0 , B \bmod 3=0 $
$A \bmod 3=1 , B \bmod 3=2$
$A \bmod 3=2 , B \bmod 3=1$
开三个桶来计数,$tong_0,tong_1,tong_2$分别存 $\pmod 3=0,\pmod 3=1,\pmod 3=2$ 。
那么来个小加法原理就有了:
小心输出格式,甚至要约分。(淦
您吊打国集
1 |
|
次次次模板题:[IOI2011]Race
刚爆踩完集训队,马上就IOI了(笑)
这题和纯模板题又有差别,在距离符合的情况下要求路径上边数最少。还是改 $\operatorname{calc}$ 。
像这种多条件下求人上人的题目,多半是平衡树或堆。
因为要求的并非 全部路径 最优的一个,而是有条件限制(距离定为 $K$ )。
所以只能打平衡树了……
吗?
人生苦短,我用 $set+lower_bound$ 。遍历所有出现过的距离,查找的是能和它拼成 $K$ 的长度中边数最少的。
因为题目大毒瘤,所以加了亿点卡常。
1 |
|
点分树(动态点分治)
“我真傻,真的,我以为三倍经验黑题躺在任务列表里就迟早会被切掉,谁知道等我切掉的时候已经掉紫了。”
处理什么问题:
带修树上点对距离查询。这里的“修”不会改变树的形态。
您会说:“我 $O(1)$ 修改,每次查询都 $O(n \log n)$ 跑一遍点分治不香吗?” 这是一种 $O(q\cdot n\log n)$ 的优秀算(bao)法(li)。
抱歉,点分树可以达到 $O(q\log n)$ 的效率。如果算上它上边套的别的数据结构(比如平衡树哇,堆哇),也一般能有 $O(q\log^2 n)$ 的高性能。
思想是什么:
想想您的暴力为什么会有这么大的复杂度。
找重心,回答询问,修改,又找重心,又回答询问,又修改……
看得出,您的做法有不少重复的操作。
尝试优(tou)化(gong)算(jian)法(liao)。
询问和修改我们都不敢偷懒,只能从找重心开刀。
我们发现,因为树的形态始终不变,找到的重心永远都是那几个。
又想到,我们每一次统计答案( $\operatorname{calc}$ ),总是在递归重心时的 $\operatorname{solve}$ 函数里。这是否表明一个重心点,它还能表示一些其他的有关答案的信息呢?
必然是可以的,我们甚至还能用取重心的搜索序建出一棵树来。这棵树就称作点分树。
接下来,我们声称:两个点在原树上的距离为他们的 真实距离 。(区别于点分树上的距离)
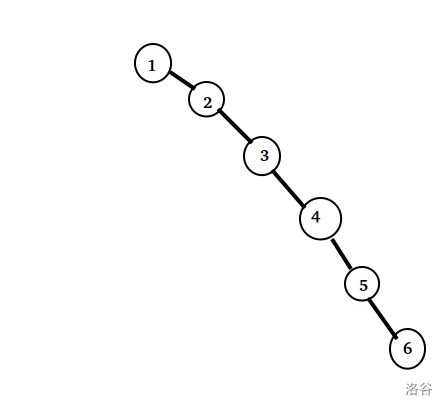
我这是一棵树(确信),树上有 $6$ 个顶点。
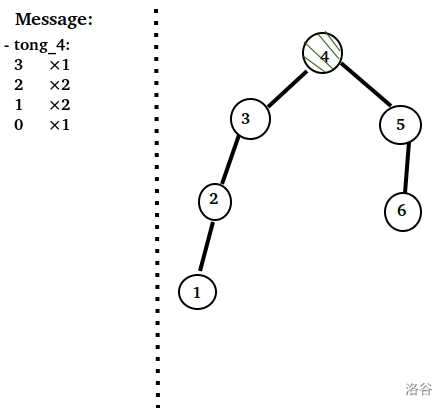
我取重心 $4$ 作为根,我开一个 $tong_4$ 装以 $4$ 为根的子树中出现的 点到根的真实距离 情况。 (右边是当前 点分树 的形态)

我取重心 $2$ 为根,距离情况再装桶。
如此往复。最终得到了图上的所有信息。

这些信息是可以在 $O(n\log n)$ 时间内得到的。下面考虑修改:
如果我们要修改原树上 $1\ 2$ 之间的边权,从 $val=1$ 改为 $val=2$ 。哪些桶里装的值会受影响?
大眼观察法, $tong_2$ 和 $tong_4$ 会受影响。
可见会受到修改的影响的,是这条边 在点分树上 的祖先们。
我们往下递归找重心时,记录一下每个重心是 从谁递归过来 的,记之为 $fa$ 。(一般点分树的题不用建出真正的点分树形态,比如像这里只要记录其 点分树上 的父亲 $fa$ 即可)。
向上跳 $fa$ ,每跳到一个点,修改相应的数据结构。 (像这里就是修改桶里的值~)
我们珂以保证:这样跳 $fa$ 可以只跳 $\log n$ 次。
原因?
点分治拥有的 $\log n$ 的优秀递归层数,使得点分树的层数也能控制在 $\log n$ 。
而查询更是轻松,只需直接调用数据结构里的信息就可了。
妙到家。
劲爆习题:
模板题: QTREE5 - Query on a tree V
其实不是很板。/kk
修改:翻转颜色,查询:给定 $u$ ,求树上距 $u$ 最近白点。
一上来就整点“好康的”。可以充分感受点分树的恶意。(bushi
查询的是最值,那就不是开桶那么简单了。
我们要开堆。
每个点必然要开一个堆,装的是它的 点分树子树 里的点,到它的 真实距离 。(因为是最 小 值,所以开小根堆)
因为有时会有白点变成黑的,无法计入答案,所以要写一个 可删堆 $AwA$ 。
这其实算得上一种小 $trick$ ,下面有放代码的。
那么修改操作即为:
一个点 $P$ 变白了 $\rightarrow$ 跳到其 点分树上 的父亲 $FA$ $\rightarrow$ 往 $FA$ 的堆里塞一个表示 $P$ 到 $FA\ $ 真实距离 的元素 $\rightarrow$ 跳到更高一级的 $FA$ $\rightarrow$ 塞元素 $\rightarrow\; \cdots$
一个点 $P$ 变黑了 $\rightarrow$ 跳到其 点分树上 的父亲 $FA$ $\rightarrow$ 在 $FA$ 的堆里删去表示 $P$ 到 $FA\ $ 真实距离 的元素 $\rightarrow$ 跳到更高一级的 $FA$ $\rightarrow$ 删元素 $\rightarrow\; \cdots$
都维护了这么多东西了,那么查询操作就有 手 就 行。我们要查询一个点 $P$ 的最近白点。
扫一遍它在 点分树 上的所有祖先。为什么是点分树?因为一个点的距离信息都保存在了它点分树上祖先的堆里,所以是在点分树上跳祖先。
取出祖先 $FA$ 位置上堆的堆顶,这个堆顶就是所有过 $FA$ 的 真实路径 中最短的一条。
这个堆顶和 $P$ 到 $FA$ 的 真实距离 可以拼起来,形成一个如树上路径 $Case\ 1$ 的两点点距。
不断上跳 $FA$ ,对点距多次取 $min$ 。最终就能得到答案辣!
1 |
|
冲高端题:[ZJOI2007]捉迷藏
是ZJOI远古题!
显然那时候浙江省选的毒瘤综合征就已经在潜伏期了。
相比上题,没有了确定的 $u$ ,而是要在全树上查最大值。
上题要考虑的范围那么小,还仅仅卡着复杂度过题,这次有那么多条边要枚举。带毒瘤,爬了爬了。
想想有没有什么“高妙”做法。
全树最大值,所以我们需要开一个全局的大根堆,维护 点分树 上的最大 点对真实距离 。记此堆为 $\mathtt{ALL}$ 。
上道题 “每个点开一个堆,装它的 点分树子树 里的点,到它的 真实距离 ” 的思路依然保留。记这些堆为 $\mathtt{subtofa[1…n]}$
但仅有一个 $\mathtt{subtofa}$ 堆无法直接维护 $\mathtt{ALL}$ 。我们可以再整一个堆用于过渡。
先更改 $\mathtt{subtofa[1…n]}$ 的定义为:“每个点(称它为 $u$ )开一个堆,装 $u$ 的 点分树子树 里的点,到 $u$ 的父亲的真实距离 ”(差别在于真实距离是到它父亲的)。
再开一个堆表示 “对于一个点 $u$ 在 点分树 中的每个儿子 $v$ ,都把 $\mathtt{subtofa[v]}$ 中最大的一个装进这个堆里”。记这种堆为 $\mathtt{fainsub[1…n]}$ 。
代码中的这句话可以彰显出其关系:
1 | fainsub[u].push(subtofa[cent].top()); |
而关于 $\mathtt{fainsub}$ 和 $\mathtt{ALL}$ ,可以看出 $\mathtt{ALL}$ 里装的东西始终为: 每个 $\mathtt{fainsub}$ 中,堆顶的 两个长度的和 (参考以 $Case\ 1$ 的形式拼接两个长度,以形成一条路径) 。
更新 $\mathtt{ALL}$ 堆的代码实现~
1 | void ins_ALL(int u) |
如果您对定义感到疑惑,这里给出一种感性理解(毕竟我也给这道题题解的各种定义看自闭过):$\texttt{subtofa}$ 维护的是纵向的距离最大值, $\mathtt{fainsub}$ 维护的是横向的距离最大值。
给出一张图助于理解:

如果点 $u$ 关灯,则将像上题一样,不断跳 $fa$ ,将 $\mathtt{subtofa[u].top()}$ 加入这个 $fa$ 的 $\mathtt{fainsub[fa]}$ ,再将新的 $\mathtt{fainsub[fa]}$ 装进 $\mathtt{ALL}$ 。
若开灯,则将以上操作改为删除元素。
自认为说的很详尽了。
1 |
|
有三倍经验 $AwA$ :Qtree4 (这题要小心带边权) QTREE4 - Query on a tree IV (我至今没卡完的常)
阴间题:[WC2014]紫荆花之恋
我 不 会(逃
以后来填坑。
无旋 $treap$
“这个splay就是逊啦!”
早就学过 $splay$ ,但每次敲完都会出锅,总是要对着板子全文比较。
导致给了窝一个刻板印象:平衡树=不行。
平衡树什么时候时候才能站起来?气抖冷。
直到窝开始盘算着学无旋 $treap$ 。
这是什么:
一种基于分裂合并操作的 $treap$ ,可以跑持久化,但不能很轻松地维护 $LCT$ 。
最重要的是,它很短。而且板子极为好背,针不戳。
思想是什么:
前置知识:知道普通 $treap$ 的形态与性质。
考虑一棵 $treap$ ,他在 $val$ 的维度上维持二叉搜索树的性质,在 $prio$ 维度上维持堆的性质。如下图:
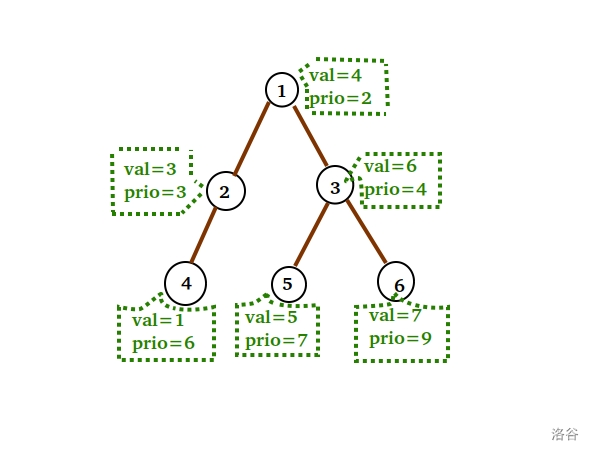
即:
其中序遍历为原序列的 按 $val$ 的有序排列(二叉搜索树的性质)
对于任何一棵子树,都满足 根的 $prio$ 值大于儿子的 $prio$ (堆的性质)
无旋 $treap$ 的特性:
_(接下来的叙述将会围绕着如何使无旋 $treap$ 完成 ”加点、删点、查第 $k$ 大、查排名、查前驱后继“ 来展开!)_
人群当中突然钻出来一个奆佬,表示发现了一个二叉搜索树的巧妙性质:
以任意一个 在值域当中的数 $val$ 为分割线,一定能将二叉搜索树分成 “小于等于 $val$” 与 “大于 $val$” 两部分,且这两部分分开来看也各是一棵二叉搜索树。
还是以原来这棵树为例,如果我们从 $val=5$ 切割:
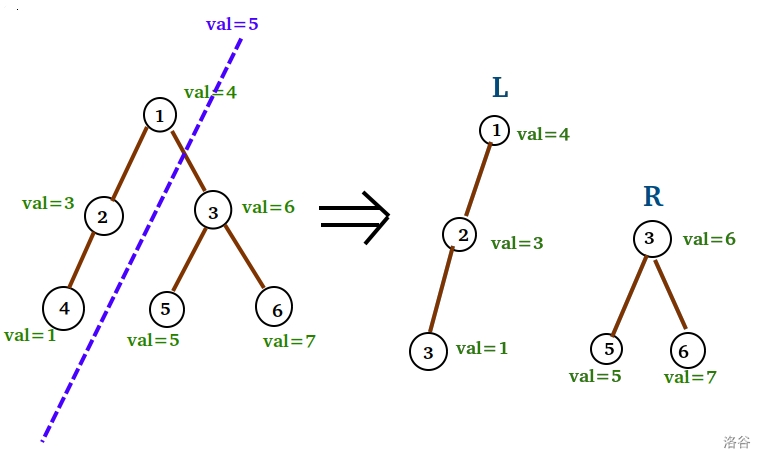
(更正:右半边 $val=1$ 的结点对应标号应为 $4$ )
我们发现这一个数就把他分( $\operatorname{split}$ )成了两棵二叉搜索树。
我们借助这一性质,来尝试进行一些操作。
加点:
首先考虑,我们直接加点时,往往只能做到把新点挂在外围。然后再经过胡乱操作( 如 $splay$ 中的 $\operatorname{rotate}$ )保送这个新点到该去的位置。
而无旋 $treap$ 则没有这样的烦恼。
倘若我们要加一个 $val=2$ 的点,我们先把原树按 $2$ $\operatorname{split}$ 出了 $L,R$ 两棵子树。
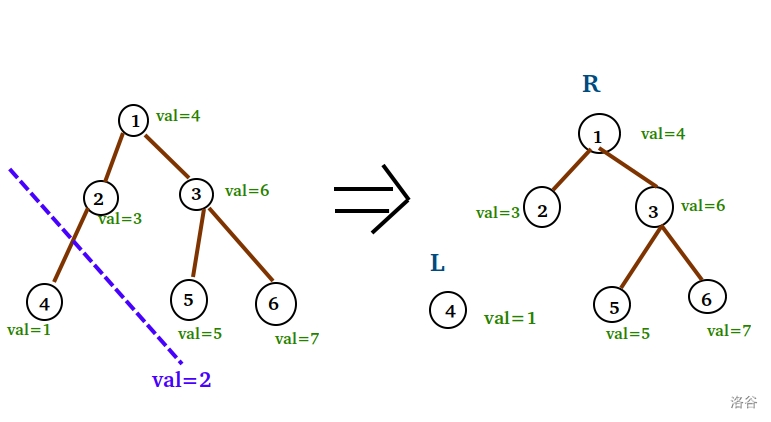
这时,我们创造一个游离的结点,保存新元素的值。
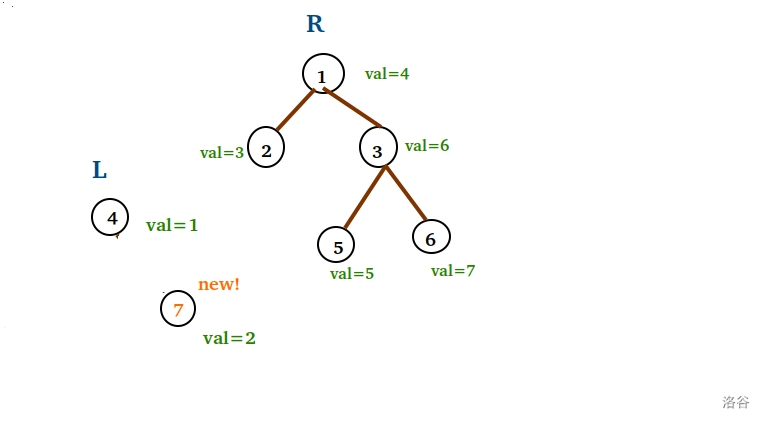
如此实现:
1 | struct node |
此时,我们发现原来的平衡树,它裂了(悲),但问题不大,我们可以想办法合并( $\operatorname{merge}$ )。
因为我们合并以后,需要仍然保持 $treap$ 的性质。故应判断需要合并的两棵树的 树根的 $prio$ 值的大小关系 。谁的 $prio$ 的更小,谁就挂在对方的下面。(怪)
这样我们先将这个游离点与左树 $\operatorname{merge}$ ,再将左树与右树 $\operatorname{merge}$ 即可~
(图被我弄丢了ToT ,或许可以使用上面那张图格物致知?)
那么,当我们在加点过程中,把一个不平衡的二叉搜索树 裂开来 ,再以一种平衡的方式 合并 回去,就能起到“制衡”的作用辣!$AwA$
该部分代码如下:
1 | void push_up(int p)//更新size |
删点:
不会真的有人删点是去把目标结点清空的吧,不会吧不会吧。
$splay$ 删点的做法是把它 $\operatorname{rotate}$ 到根然后往虚空里一丢。
可无旋 $treap$ 之所以叫“无旋”,就是因为它没有旋转的操作。
我们充分利用无旋 $treap$ 的特性,大力将要删的结点 $u$ 从全树上 $\operatorname{split}$ 出来,再将 除去 $u$ 的剩余几部分 大力 $\operatorname{merge}$ 回去。最终就能收获一个不带 $u$ 的新树辣!
图示如下 $AwA$ :(假设我们现在要删值为 $x=6$ 的点)
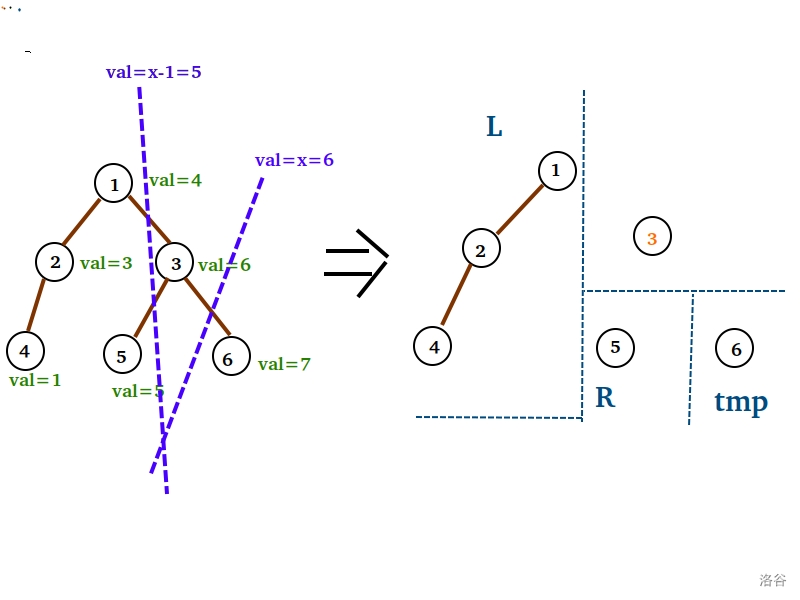
先裂开来。再排除 $val=x=6$ 的 $3$ 号点,进行如此合并。
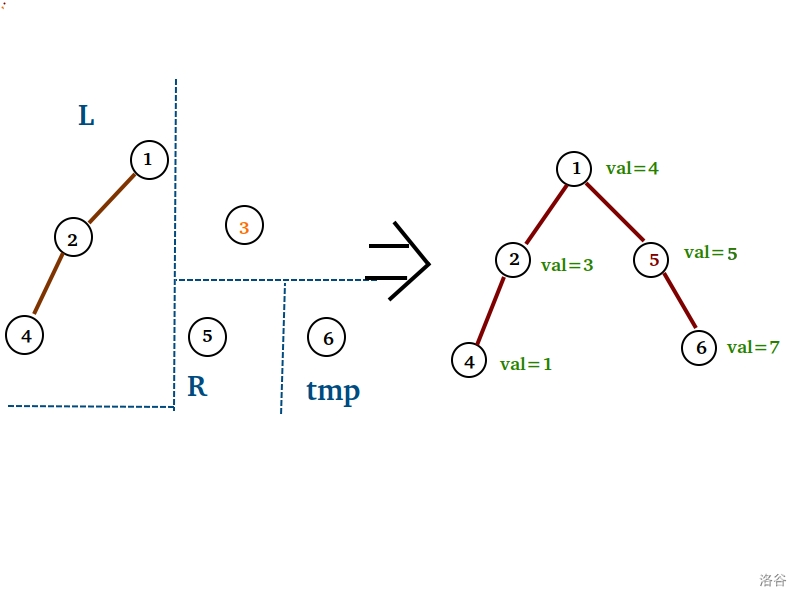
这部分的代码实现~
1 | void erase(int x) |
为什么只用担心 $R$ 的儿子分崩离析?
因为他的位置很尴尬,他的左儿子可能会被 $x-1$ 的一刀砍断,右儿子可能会被 $x$ 的一刀砍断。(惨 R 惨)
查第 $k$ 大:
因为这是一棵二叉搜索树,所以用脚想都知道一种可行的方法是中序遍历再查。
而且这种方法复杂度还不赖,甚至有 $O(n)$ !(暴力之耻)
可是你清醒一点,这是一棵平衡树,他的常数不可谓不小。
再者说之后我们的 $pre$ 和 $nxt$ 函数也要用到它(好像有点剧透?)。
我们希望找到一个复杂度优秀的做法。
我们突然想到,我们 $treap$ 的结点信息里,似乎还保存了一个 $size$ 变量。
$\color{black}\mathtt{D}\color{red}\mathtt{Pair}$ 神说过,优化的第二种方式是 “可并的操作一起处理” 。
如果我们明明知道左子树里根本没有 $k$ 这么多个元素,也就不可能存在第 $k$ 大的数。那我们凭什么往里面去递归。
这 给 了我们一个启发,根据 $size$ 确定递归范围,逐层找到对应位置。
代码实现如下~
1 | int getkth(int p, int K) |
获取元素排名:
这一操作用的不多,随便口胡一下(逃
我们把一个元素以它的 $val$ 值 $split$ 出来。这时人群当中钻出来一个 $dalao$ ,他说:“我知道了,$L$ 树里的元素全都是比它小的!”
u1s1,qs。
有 $T[ls(p)].size$ 这么多的元素比它小,那么显而易见地,这个元素的排名就是 $T[ls(p)].size+1$ 。
别忘了 $\operatorname{merge}$ 回去。
代码如下~
1 | int getrank(int p, int K) |
查前驱:
我们之前提(剧透)到查前驱也是要用到查 $k$ 小值这一操作,想必各位一定已经YY出了做法了吧。
实则很简单,我们查前驱,实则就是要找小于 $x$ 的元素中,最大的一个,我们把小于 $x$ 的部分 $\operatorname{split}$ 出来后,取出这一部分的第 $T[L].size$ 位元素就可了。
别忘了 $\operatorname{merge}$ 回去。
1 | int pre(int x) |
查后缀:
后缀与前驱同理,不多加赘述:
1
2
3
4
5
6
7
8
int nxt(int K)
{
int l, r;
split(ROOT, K, l, r);//将大于x的部分分离出来
int ans = T[getkth(r, 1)].val;//取第1位
ROOT = merge(l, r);
return ans;
}
1 | int nxt(int K) |
得,这就是无旋 $treap$ 吗,i了i了。
劲爆习题:
模板题:【模板】普通平衡树
板子题首当其 冲 !
要求的就是之前的六个操作,码一遍就 VAN 事了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
using namespace std;
const int MAX = 1e5 + 7;
int N, ROOT, cnt = 0;
struct node
{
int son[2];
int fa;
int val;
int prio;
int size;
} T[MAX];
/*创造新点*/
void add(int x)
{
cnt++;
T[cnt].size = 1;
T[cnt].val = x;
T[cnt].prio = rand();
ls(cnt) = rs(cnt) = 0;
}
/*整合子树信息*/
void push_up(int p)
{
T[p].size = T[ls(p)].size + T[rs(p)].size + 1;
}
/*分裂*/
void split(int p, int x, int &L, int &R)
{
if (!p)
{
L = 0;
R = 0;
return;
}
if (T[p].val <= x)
{
L = p;
split(rs(p), x, rs(p), R);
}
else
{
R = p;
split(ls(p), x, L, ls(p));
}
push_up(p);
}
/*合并*/
int merge(int Lroot, int Rroot)
{
if (!Lroot)
{
return Rroot;
}
if (!Rroot)
{
return Lroot;
}
if (T[Lroot].prio < T[Rroot].prio)
{
rs(Lroot) = merge(rs(Lroot), Rroot);
push_up(Lroot);
return Lroot;
}
else
{
ls(Rroot) = merge(Lroot, ls(Rroot));
push_up(Rroot);
return Rroot;
}
}
/*插入操作*/
void insert(int x)
{
int l, r;
split(ROOT, x, l, r);
add(x);
ROOT = merge(merge(l, cnt), r);
}
/*删除操作*/
void erase(int x)
{
int l, r, p;
split(ROOT, x, l, p);
split(l, x - 1, l, r);
r = merge(ls(r), rs(r));
ROOT = merge(merge(l, r), p);
}
/*查第K大*/
int getkth(int p, int K)
{
if (K <= T[ls(p)].size)
{
return getkth(ls(p), K);
}
if (K == T[ls(p)].size + 1)
{
return p;
}
return getkth(rs(p), K - T[ls(p)].size - 1);
}
/*获取排名*/
int getrank(int p, int K)
{
int l, r;
split(ROOT, K - 1, l, r);
int ans = T[l].size + 1;
ROOT = merge(l, r);
return ans;
}
/*获取前驱*/
int pre(int K)
{
int l, r;
split(ROOT, K - 1, l, r);
int ans = T[getkth(l, T[l].size)].val;
ROOT = merge(l, r);
return ans;
}
/*获取后继*/
int nxt(int K)
{
int l, r;
split(ROOT, K, l, r);
int ans = T[getkth(r, 1)].val;
ROOT = merge(l, r);
return ans;
}
int main()
{
srand(20050418);//窝npy的生日ww
int Q;
cin >> Q;
while (Q--)
{
int opt, num;
cin >> opt;
if (opt == 1)
{
cin >> num;
insert(num);
}
if (opt == 2)
{
cin >> num;
erase(num);
}
if (opt == 3)
{
cin >> num;
cout << getrank(ROOT, num) << endl;
}
if (opt == 4)
{
cin >> num;
cout << T[getkth(ROOT, num)].val << endl;
}
if (opt == 5)
{
cin >> num;
cout << pre(num) << endl;
}
if (opt == 6)
{
cin >> num;
cout << nxt(num) << endl;
}
}
}
1 |
|
EX-模板题 :【模板】文艺平衡树
CSP到了,我向佛祖许愿,希望我的平衡树能实现区间翻转。
佛说:“我的正解是 $splay$ ,那你这在无旋 $treap$ 上如何实现?”
我说:“无旋 $treap$ 的区间处理能力之强。它可以用两次 $\operatorname{split}$ 轻松取出一段区间。”
“ splay 做得到吗?”(拉狗行为)
佛说:“你翻转了区间,那你这还能叫二叉搜索树吗,你的 $\operatorname{split}$ 不是废了?”
我说:“我的 $\operatorname{split}$ 是按 $size$ 分裂的,这样才可以确定这个区间在原序列上的位置。”(详见代码)
佛说:“不行,单单只是取出一段区间来个 ODT 也能做到,你有什么好说的。”
我说:“那就打一下 $tag$ 。同一区间翻转两次=全部木大。”
佛说:“不行,我这是一棵平衡树,又不是什么线段树。”
我说:“那我就把标记,打在 分离出来的区间 的根上,到时候标记下传的时候只需要一番大力 $swap$ 。”
佛说:“不行,我还是不知道怎么打标记。”
我说:“那就来一张图演示一下这一流程。”
(本图不代表最终要操作的序列,但不影响观看)
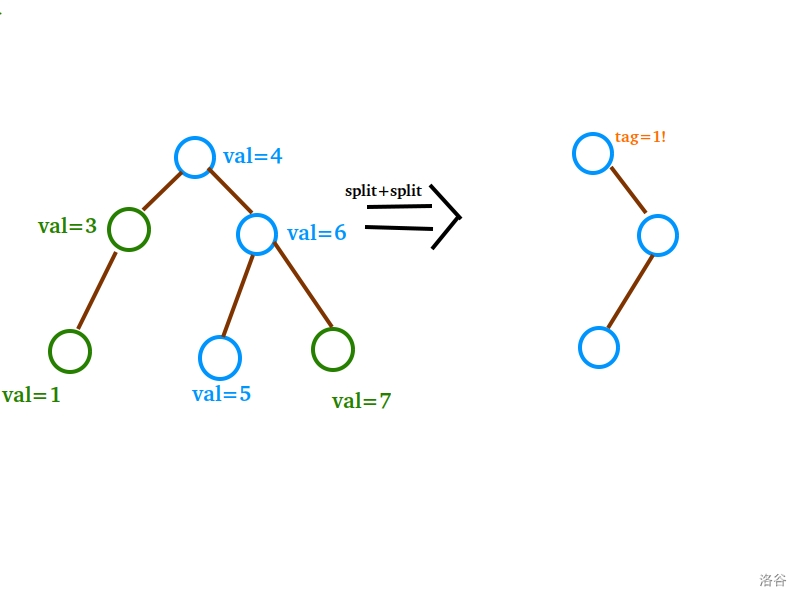
佛说:“不行,我不知道什么时候该下传标记。”
我说:“打过线段树的都知道,不到 修改 或 查询 的时候是不用 $push_down$ 的。这里也是如此。”
“修改是没有什么用得上下传标记的地方的,毕竟每次我们分离出一段区间的时候,往往只是在这里打个 $tag$ 。从来没有 影响过其他地方 的 $tag$ 。”
“而查询,基于 『二叉搜索树的中序遍历是它所代表的原序列』 这一重要思想,我们应该在输出的时候 $push_down$ 就可以了。
佛说:“不行,那你这 $push_down$ 函数里面要干什么事情。”
我说:“我们观察到,翻转一个区间,可以看作是一个位置为对称轴,将一段区间 左右翻转 得来。”
“知道了这一个条件,我们有了一种强烈的意识,在平衡树上交换一个结点的 左右两孩子 ,等价于在序列上将一个元素的 左右两边交换 。”
佛说:“我不信。”
我说:“手模一下不是有手就行?”
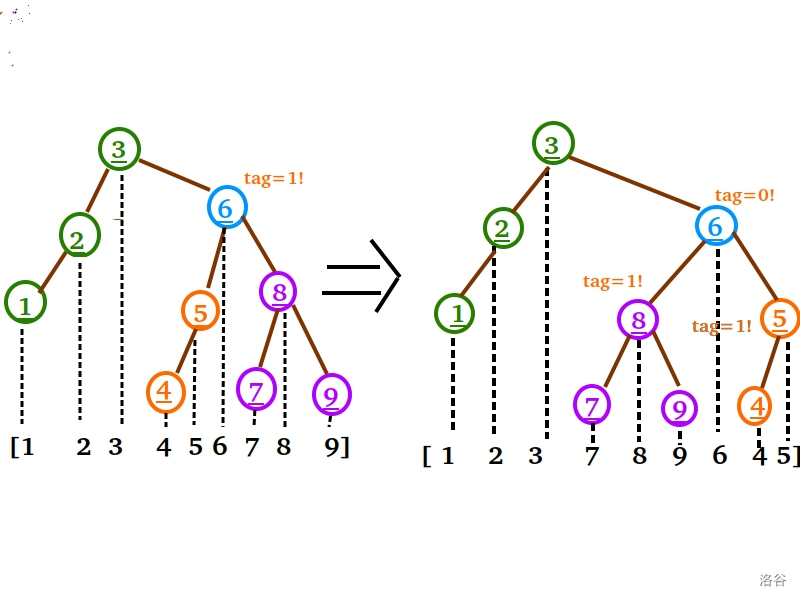
“我们先把6号结点的 $tag$ 先处理了,再把标记往下传,递归进行 ‘交换左右儿子’ 这一动作直到叶子结点不就是了。”
佛说:“不行,我是伸手党,我要看代码。”
我说:“彳亍。”
1 | void push_down(int p) |
佛哭了,说:”这样就能AC了。“
1 |
|
次模板题: [NOI2004]郁闷的出纳员
一道深刻考验选手对无旋 $treap$ 内层原理的(毒瘤)好题。
这题要求:1.全局加减 $k$ ,2.删去小于 $val$ 的所有元素 ,3.插入一个元素 , 4.查询第 $k$ 大。
首先一眼发现,因为加减都是全局加减,所以根本没有必要真的加在每一个元素上,随手开个 $delta$ ,表示 全局的改变量 。
而剩下与数值有关的,只有一个 “删去小于 $val$ 的所有元素” 操作了。
因为我们手上有 $delta$ ,我们可以顺理成章地把这一操作看作 “删去小于 $val-delta$ 的所有元素” 。
_(以元素值为参考系(误),元素值增加了delta,可以看作是这个val减小了delta)_
“真正的勇士,敢于面对直接枚举元素的复杂度。”($\times$)
“真正的勇士,敢于面对 TLE 0 。”($\surd$)
你意识到无旋 $treap$ 的 $\operatorname{split}$ 的作用就是将原树分成 “ 小于等于 $val$ ” 与 “ 大于 $val$ ” 两部分。
那我们以 $val-delta$ 分,不就可以让我们分离出来的左树,装的都是小于 $val-delta$ 的元素了?
分离完了以后直接使 全树的 ROOT 等于右树的根 ,相当于把左树里这些小于 $val$ 的数全部逐入虚空。
这样便可实现删点。
代码如下:
1 |
|
网络流基础建模——最大流
这里讲的不是实现,只是一些套路。
都0202年了,不会真有人认为网络流都是套路题吧?
哦是我啊那没事了。
套路一:构建超级源汇:
有的题目,他告诉你谁和谁之间有阿巴阿巴的路径,但硬是不告诉你谁是源,谁是汇。
这时候,朴素的最大流思想可能就会陷入僵局。
但是我们有超级源汇的思想。
我们 创建一个新点 ,称其为源。
向所有该连的点连边。
汇的思想同理。
建一张图就像这样:

可以看出,这一思想用于处理 “你……,他……,而我……,我们都有全局的贡献” 的问题。
下面来看这个命题:
_RUI_R有了去NOI和APIO的资格,zjjws有了去WC和APIO的资格,而我有了去加里敦参加夏令营的资格,我们都有对XJ的贡献。试问,如果一个人只能去打一场比赛,XJ能收获多少参赛名额。_
一眼看出,这是典型的多源多汇模型。
把每个人和自己能参加的比赛连边,这时相当于是跑一个 二分图最大匹配 。
而我们要以网络流的思想解决,则需要 开一个超级源,向所有人连边,开一个超级汇,让所有比赛向它连边 。

这里超级源连出去的边容量为1,即 限制了每个人最多 只能打一场比赛 ,也就是 从一个人流出的流量最多为1 。
这启发我们,超级源汇在连边时可以有意无意地起到 限流 作用。
劲爆例题:
典型的二分图最大匹配,一边是英国飞行员,一边是外国飞行员,如果俩人能打配合,就在俩人之间连边。
随手像上面那样建一张图。
这时我们发现,外国飞行员也是人,他也只能和一个人进行配对。
外国飞行员 使用分身术,出现了一个新的 外国飞行员
所有右边的点向超级汇的连边,容量改为 $1$ 。
这样我们就建出了一张图,在这张图上跑一个最大流就珂以了。
代码如下:
1 |
|
套路二:最大流改最小割:
窝非常擅长鸽。
有的题目,他告诉你选了阿巴阿巴就不能选阿巴阿巴。
这时候,朴素的最大流思想可能就会陷入僵局。
但是神仙们证出了最大流等于最小割。
这个问题就转化成了,我 放弃选一些东西,使我剩下的收益最大 。
考虑全图中从源点到汇点的一条路径,假设这条路径是由 好几段拼成 的。
我想把它割断至无法通流,则必然是割断其中的 某一段 。这个“割断”的过程,实则就是相当于 放弃了这一段的收益 。
而这条路径上的其它几段得以保留,所以我能获得剩下的这些收益。

这时,存在两条路径从源点通往汇点的路径,我们要把他们割断,一种可行的做法是割断 $value_{\ 5}$ 使剩下4个 $value$ 得以保留。
当然,还存在一种做法是割断 $value_1,value_3$ 使剩下三个得以保留。
此外,在有的题目中,有的利益是固定利益,是无法丢弃的,这时,我们就可以将这条边的容量设为 INF 。
可以看出,最小割模型非常善于处理 “可以……,但是你得……,这一切值得吗?”的问题。
下面来看这个命题:
_“我告诉你,但是你得跟我搞姬,这一切值得吗?”_
我们可以看出这里存在一个约束关系, “ 我可以得到题解,但是我有翻车的危险,即‘失去了安全’ ”。
那么很显然我们可以建出一张图,像这样:

颜色好评,如果我们选择了题解,那么我们就会失去开车的安全;反之同理。
劲爆例题:
首先,一眼看出模型,“我可以选这个点,但是我就选不了周围这些点了,这一切值得吗?”。
那么我们随便挑出两个相邻的方格,都可以建出这样的图。
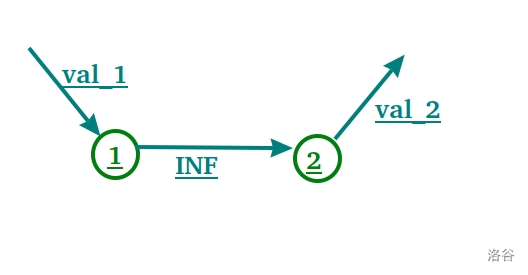
表示要么选 $val_1$ ,要么选 $val_2$ 。
如果我们对于每一个点建一张如上例的图,最终的成品就是这个玩意。

这时我们发现,这张图根本没有源和汇。/jk
但是我们的内心毫无波澜,甚至一眼出了 超级源汇 的思想。
可超级源汇的模型也不是用脚造的,我们需要决定 谁去连源,谁去连汇 。
想起了之前飞行员配对的做法,我们可以把这些点分出一张 二分图 。
二分图的要求是同一部分内 无连边 。正难则反,什么点之间有连边?显然是相邻的点。
那么,无连边的部分,必然是那些不相邻的。
这时,我们就可以用黑白染色的方式,建出如下的图。

此时,随便挑出一条路径来,依然满足 最小割 的样式,可以在这上面跑最大流,来求出这一 最小的舍弃价值 。
而我们收获的价值,就是 所有价值总和-舍弃的价值 。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
using namespace std;
const int MAX = 1e5 + 7;
const int INF = 1e18;
/*dinic组件*/
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
void bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
if (dep[T])
{
flag = 1;
}
}
int dfs(int u, int in)
{
if (u == T)
{
return in;
}
int out = 0;
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
if (in == 0)
{
return out;
}
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
int M, N;
int idx(int x, int y)//获取一个方格的编号
{
return (x - 1) * N + y;
}
signed main()
{
cin >> M >> N;//这道题对N,M的定义是和常识相反的
//申必题(bushi
int sum = 0;
S = 0, T = 107 * 107 + 1;
for (int i = 1; i <= M; i++)
{
for (int j = 1; j <= N; j++)
{
int num;
cin >> num;
sum += num;
if ((i + j) & 1)//若行+列=奇则染白,连源点
{
adde(S, idx(i, j), num);
adde(idx(i, j), S, 0);
/*向上下左右四个方向连边*/
if (i > 1)
{
adde(idx(i, j), idx(i - 1, j), INF);
adde(idx(i - 1, j), idx(i, j), 0);
}
if (i < M)
{
adde(idx(i, j), idx(i + 1, j), INF);
adde(idx(i + 1, j), idx(i, j), 0);
}
if (j > 1)
{
adde(idx(i, j), idx(i, j - 1), INF);
adde(idx(i, j - 1), idx(i, j), 0);
}
if (j < N)
{
adde(idx(i, j), idx(i, j + 1), INF);
adde(idx(i, j + 1), idx(i, j), 0);
}
}
else//若行+列=偶则染黑,连汇点
{
adde(idx(i, j), T, num);
adde(T, idx(i, j), 0);
}
}
}
int ans = 0;
while (1)
{
flag = 0;
bfs();
if (flag == 0)
{
break;
}
ans += dfs(S, INF);
}
cout << sum - ans << endl;//收益为总价值-割
}
1 |
|
套路二-进阶:其他黑白染色模型:
上文的方格取数问题,可以归为一种黑白染色模型中的典型。
而解决这种问题,其要义在于构建一种可行的方式,将所有玩意分成两堆,使得任何 黑点与白点之间都没有直接连边 。
听上去很 $simple$ ,实际上的确很 $naive$ 。
就随便挑一道题来看叭~
_以下只阐述如何染色,其他实现细节在此不提_
就用题目上的原图好了。
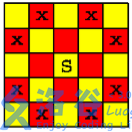
我们发现 $S$ 在一个黄点,而他的下一步必然是一个红点。(由图可知)
那么我们像方格取数一样,按 (行+列)的奇偶性 黑白染色即可。
\
那个表情是超链接……
长脖子鹿不会被别马腿因为长脖子鹿只有鹿腿哈哈哈哈哈哈哈
其实一点也不好笑
这道题面里还是有图,我们还是征用题面里的图。
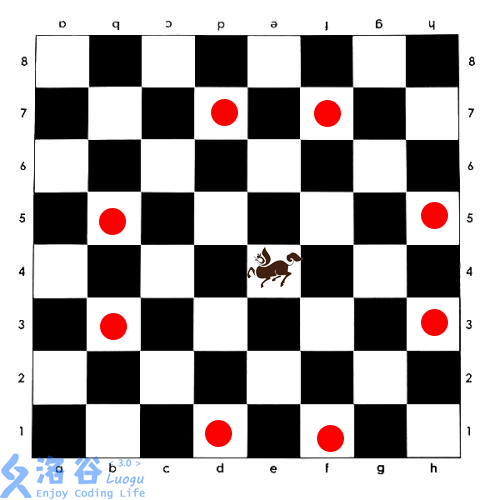
可以看到这里,一个白点会跳到另一个白点上。我们之前(行+列)奇偶性染色法就不行了。
但我们会想出新方法切了这道题。
因为长脖子鹿跳一下是 $2\times 4$ 的,我们发现,行和列加的都是偶数, 不影响其奇偶性 。
也就是说,奇行和偶行之间不会有连边。
所以我们将 奇行染黑,偶行染白 即可。
高质量好题/se/se/se(指题面
王固然是天下第一,但是这道题出题人也是脑洞真的大。
我们看见,每隔两秒周围四个地方的宝石都会消失。而这两秒之内我们能干什么,一秒踩在一块有宝石的砖上吸走了宝石,下一秒在一块空砖上赶路前往下一个有宝石的地方。
也就是说,我们吸走了一个地方的宝石, 周围四个位置 都是必然拿不到了的。
然后,就变成方格取数问题了???
我直接震惊。
- 有一道叫 [国家集训队]部落战争 的题,看上去很像黑白染色,事实上他是最小路径覆盖问题。我们之后会提到。
套路一+套路二=套路三:最大权闭合子图模型
“有的题目,他告诉你必须得选阿巴阿巴才能选阿巴阿巴。有时候选阿巴阿巴可能带来负收益。”
这和套路二的最小割模型没有什么区别,如果你是语文王子,你会发现上面这句话其实和套路二表达的是同一个意思。
只不过让人以为这里仿佛有负边权,然后自闭。
我们换一种说法:对于一个正收益的东西,我们要么 得到这个价值 ,要么 省下“得到这个价值”所需要的钱 。
由此一来,最小割的思想就呼之欲出力。

即:要么获得价值 $value$ ,要么赚回花费 $cost$ 。
由于一个正收益的物品,可能需要很多种的 前置花费 ,同时,一个负收益的物品可能同时成为很多物品的 前置花费 。
所以我们常常会用到超级源汇的思想 $qwq$ 。
不难看出,最大权闭合子图模型适合解决 “tyy讲题” 类型的题。
(生动比喻了有一大堆前置知识的数论 浅 谈)
我们来看下面这个命题:
tyy在讲课,今天他要讲的是杜教筛和min25,其中,杜教筛需要莫反和积性函数的前置知识,min25需要多项式和积性函数的前置知识,学这些前置知识需要你爆掉一定的肝,但是学一个新科技筛法又可以恢复一定的肝,求自己最大收益。
一眼发现有 “前置知识” 这一 有 趣 的玩意。
我们把杜教筛单独拉出来看,有下面的最小割模型:

(颜色好评)
表示我们要么去学杜教筛 $val_{mifafa}$ ,要么省下 $cost_{mobius}+cost_{multi}$ 的花费。
而放之全图就像这样:
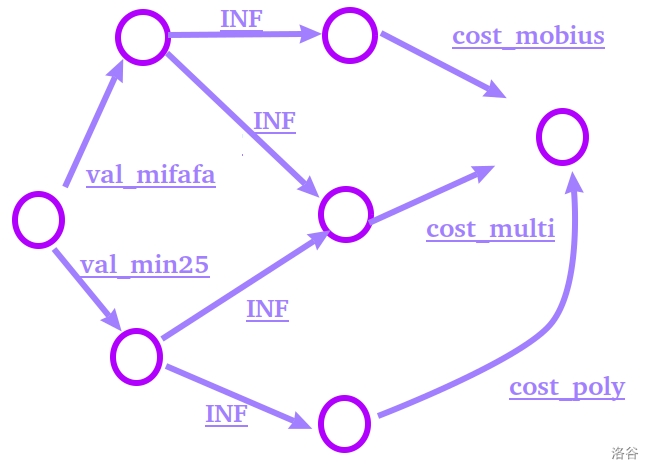
迫真英语翻译。
这样,我们就可以跑出全图的最小割辣。
但是,我们此时不能直接用总价值减去最小割来求解。
我们此前称学习前置知识的价值,是 我们省下了多少肝 。
可我们什么也不学,他又不会白送我们这些肝。换言之,这些肝本就不是我们应得的。
我们本该得的,是学这些筛法所收获的科技知识。
明明是你自己要偷懒护肝的。
所以我们应该用所有筛法的收益之和,减去最小割,这才是我们最终的答案。
劲爆例题:
一眼看出,我可以获得拍一张照的价值,但是我有带几个人的前置条件。
这很容易就转化为了 最大权闭合子图 的模型。
用脚也可以造出同上例一样的图。
(其实用本题样例建出来的图和上一张图是一模一样的。)
然后按部就班做就VAN事了。
1 |
|
套路四:拆点
“有的题目,他告诉你他要最大收益,但是一个物品只能用阿巴阿巴次。或者他要最小割,但是割的是点,不是边。”
这是,朴素的最大流/最小割就会陷入僵局。
但是拆点是一个好 办 法。
拆点的要义是:把一个点拆成 入点 和 出点 两个点,在这两个点之间连上一条 一定容量 $limit$ 的边。
这样,任何时候,通过这个点的流量都只会控制在 $limit$ 之内。
老百度网盘了
具化到图上,如果我们需要控制通过一个点的流量永远不超过 $limit$ ,则有:

$in$ 和 $out$ 都是从同一个点上拆出来的,我们让通过这个点的流量不超过 $limit$ ,实际上就可以把 $in$ 和 $out$ 之间这条边的容量限为 $limit$ 。
不难看出,拆点模型适合处理“购买超级会员享受8倍速度” 的百度云 限流 行为。
来看下面这个命题:
XJ地形可以简化成一张有向无环图。在结点处,会站有值周班同学检查。此时,在他面前跑过的人 禁止超过 $W_i$ 。现在给出每个结点处的检查情况,试求最多有多少学生能在去食堂的路上跑步。
很显然,这里有明显的限流现象。( 指站在一旁看着高一学生 rush )
从一个检查点到另一个检查点是随便你怎么跑的,从XJ中学12:20时的情况便可知晓。
言外之意是, 边 上的限流为 $inf$ 。
而对于一个点上的限流,我们把一个点拆成一个出点和一个入点,两点之间连长度为 人数限制 的一条边。
这样,我们就能建出这样一张图:

在这张图上,我们就可以做到通过每个检查点的人数不超过 $limit$ 人。
可以注意到的是,图上源连的是入点,汇连的是出点,前一个点的出点连的是后一个点的入点。
而这张图上的最大流,就是本题的答案。
劲爆习题:
[USACO5.4]奶牛的电信Telecowmunication
之前是拆点求最大流,而现在是拆点求最小割。
不能割边,则把所有边的边权设成 $inf$ ,这是无可厚非的。
因为我们割的是点,而点在网络流上不好处理,所以我们把一个点拆成两个点,两点之间连容量为 $1$ 的边。
为什么连边权为 $1$ 呢?
我们割一条这种边,相当于我们拆了一台电脑。(可怜的 FarmerJohn /dk)
而题目要求的是拆电脑的数量,那么设边权为 $1$ ,可以正好反映拆的数量。
答案即为全图的最小割。
代码如下:
1 |
|
套路一+套路四=套路四点五:网络流与LIS
有的题目,他让你求 LIS 的条数 ,或者让你求删去哪个数会使 LIS 的值改变 。
这里的 LIS 实则是泛指所有转移方程为 $dp[i]=dp[j]+1$ 形式的 $dp$ 。
为什么称其为四点五是因为这一类型的题太少了,但是的的确确是一种新模型。给他一个面子。
我们直接丢出例题:
问题一:求一个序列上 LIS 的长度。
问题二:试求一个序列上 LIS 的条数。其中元素不能多次使用。
问题三:试求一个序列上 不同的 LIS 的条数。其中 $1$ 号和 $N$ 号元素可以多次使用。
末 日 三 问
在《导弹拦截》那里 打过炮 的人应该会知道,LIS 有一个 $O(n\log n)$ 的优秀做法。
不会也没有关系,因为这道题只能用 $O(n^2)$ 做法。
求 LIS 的 $n^2$ 做法,状态转移方程如下:
$dp_i$ 代表:到 $i$ 位置时的最长上升子序列。
我们之所以用这种 $n^2$ 方法,是因为我们要知悉每一个位置对应的 $dp$ 值。
一个 $dp$ 值为 $x$ 的位置,肯定能建出一条长为 $x$ 的路径,它是一条以 这个位置为结束 的 上升子序列 。
而这条路径上的每一条边,必然从 $dp$ 值 低的位置 连向 高的位置 。
这很好证明。如果从高的位置 $i$ 连向低的位置 $j$ ,有 $dp_i>dp_j$ :
$i$ 之前必然拖着一条长为 $dp$ 的 上升序列 。而 $dp$ 值低顶多只顶得住 $dp_j$ 的长度,却承受不住 $dp_i$ 。(破路)
我们便可以以此,用 $dp$ 值分层,建出一张分层图:

我们推知这条序列的 LIS=3 。
也就是说,数一数这张图上有几条长为 $3$ 的路径,其中一个点只可以使用一次。(唐突数数)
这时,我们可以 转动脑髓,发动眼光 ,自己去构造网络流图,使得这一答案能被跑出。
因为是限制了通过 点 的流量,所以我们应该用套路四中的 拆点。把一个点拆成一个入点和一个出点,两点之间连容量为 $1$ 的边,表示限流为 $1$ 。
因为元素和元素之间没有什么限制,所以其他边容量为 $inf$ 。
而 $dp=1$ 和 $dp=LIS$ 的元素可能有多个,所以需要用到 超级源汇 的思想。将 $dp=1$ 的连源, $dp=LIS$ 的连汇。
最后跑最大流出答案。
而第三问,则只需要将 $1$ 号和 $N$ 号元素出入点之间的容量设为 $inf$ 即可。
实现如下:
1 |
|
套路五:最小路径覆盖问题
有的题目,它给了你一张DAG,要求你用最少的路径去覆盖它上面的每一个点。
听上去有、抽象,看来出题人也是 抽象人 。
我们通过画图来解释这一问题:
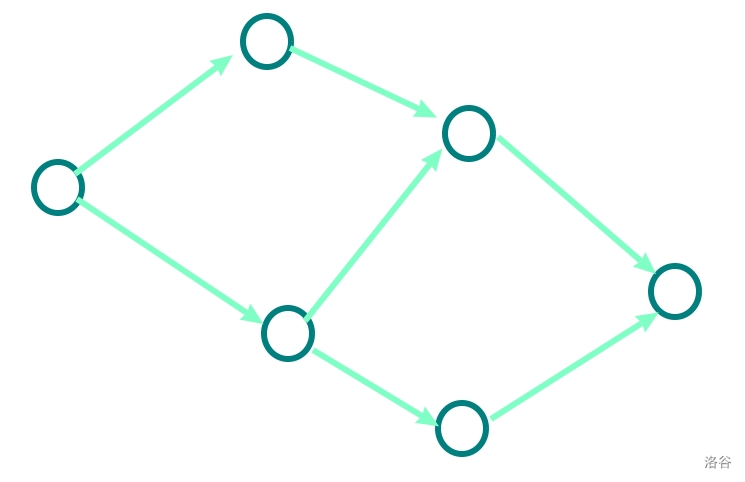
这是一张普通的 DAG 。
我们每次选择一条任意长度的路径,并将路径上的所有点染色。
如下是一种方法:

RT,粉、黄、蓝三条路径使得所有点被染色。这时我们使用的路径数量=3。
然而但凡有一点脑子的人都能看出,这条黄色路径是完全不需要的,我们用2条路径照样可以覆盖,如图:

而最小路径覆盖问题,就是解决“ 找到用最少路径覆盖全图的方案 ”这一问题的。
我们如何用网络流实现这一过程?这就要用到 最小路径覆盖模型 力。
先假设你是一个铁憨憨。你把每个点都用一条长度为 $1$ 的路径给覆盖了。
这时来了个 神仙 ,看到你的覆盖方案,非常 $angry$ ,把你代码给删了。
她说你怎么这么蔡,很多点明明可以合并以减少路径数。
你感到非常委屈,说凭什么。
她扔出一个定理:“一张图中,如果一个点只能用在一条路径上, 路径数=点数-点之间匹配数 。”
“这个很好证明。因为当点之间没有边时,每个点都需要一条路径去覆盖他, 路径数=点数 ;一旦有一条边(x,y)时,相当于能把这两个点合在一起,用 一条路径 去覆盖他们俩,所以 路径数=点数-1 ;以此类推。”
你惊了,“那不就转化成了一道最大匹配了嘛。”
的确,但是这里依然分不出二分图来。我们需要 奇技淫巧 。
把一个点拆成入点和出点,永远是入点向对应的出点连边,就可以保证建出一张二分图来:
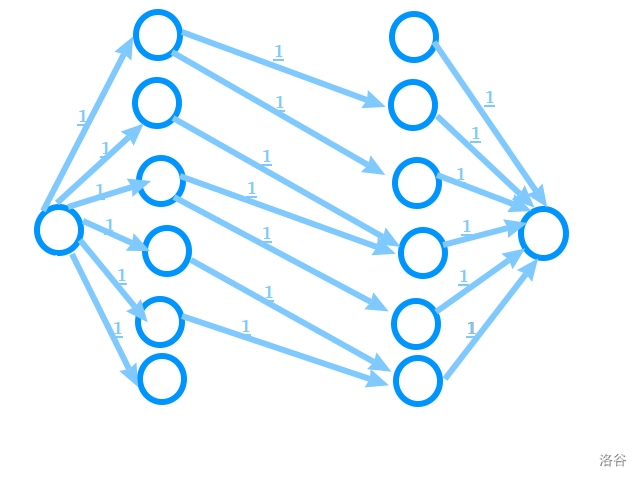
这是之前那张 DAG 建出来的图。
我们需要的是匹配数,所以图上所有入点和出点之间连的边,容量均为 $1$ ;超级源和超级汇连出的边,容量也均为 $1$ 。
这样跑最大流的答案就是 最大匹配数的数值 辣!
所以这就是一道最大匹配题了。
这便是最小路径覆盖的基本算法。
不口嗨了,直接上例题:
这时,我们想起了之前提到的一道在讲黑白染色时提到的 不讲武德的 题目:
你以为这是一道黑白染色,只是跳的规则不固定了而已?
那还是大意了呀。
黑白染色题(如方格取数),并没有要求每个点都要被取中。而这里需要。
我们从上往下推进,因为不能回头,所以我们的推进从最顶上一行开始,到最底下一行结束。
而这个推进的过程,要 覆盖所有的点 。
这时,便可以用到之前的最小路径覆盖模型了。
先画 DAG ,点与点之间,可达即连边。
再套最小路径覆盖即可。
(实则这两步可以合成一步做)
希望国集好自为之,不要搞窝里斗。
1 |
|
EX-套路五:其他有趣(?)的最小路径覆盖问题泛讲:
天底下哪有裸的网络流,从来都是老阴比居多。
这一现象在“最小路径覆盖问题”上得到了充分的体现。
因为最小路径覆盖的板子局限性太高了,所以他的 变体 也就特别的多。
这就和 “因为NEKOPARA官方给时雨的戏份太少,导致时雨的本子特别多” 是一个道理。
我们挑几个范例,来剖析一下出题人的良(sang)苦(xin)用(bing)心(kuang):
你的正解不是搜索,ko no 网络流 da !
首先,我们制定一个总体的计划,逐个地放小球,直到放不下了为止。这时就是答案。
其次,我们想想这是怎么套上最小路径覆盖的。我们把每个球看作一个点,把两个 相加之和为完全平方数 的小球,所对应的点之间连边。
这也代表着我们以数 $a$ 为某柱子的顶端,我们就 可以 去转移到下一个与 $a$ 有连边 的数 $b$ 。
建出一张图来就像这样:
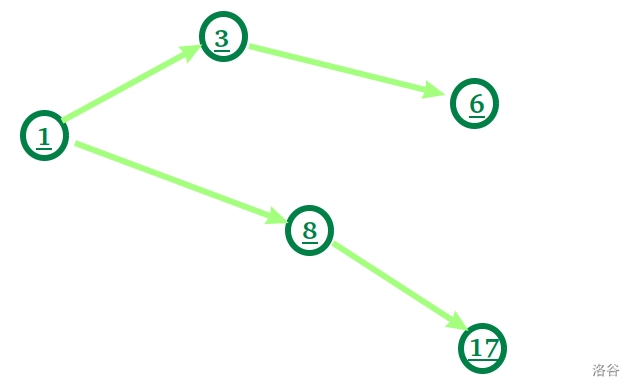
当我们把 $1$ 放在一个柱子的顶端,在他的上面,我们可以去放 $3$ ,也可以去放 $8$ 。
在图上,相当于我们在 $1$ 这个位置,可以走到 $3$ 也可以走到 $8$ 。
就这样走着走着最终会走出一条路径,这条路径上的每两个邻点之间都 有边相接 ,意味着相加为完全平方数。
这样的一条路径正好对应了一根柱子。
那做法就很显然了,一个一个加小球,连边,当加某一个小球时,跑出的最小路径覆盖条数 超过了柱子数 ,那这就是答案。
网络瘤少有的黑题,其实还是好打的。
是什么让我们想到这是一道 “最小路径覆盖问题” ?
题解(闭嘴)
题目中提到“可以增开任意架飞机”,而求的是“最少使用的飞机数”,一个飞机会经过许多点……这使我们想到“最小路径覆盖”。
“最小路径覆盖”需要有 DAG ,否则就是白给。
谁设为点,是机场吗,呐?
一个机场可能多次接收航班,多次送出航班,也就是说一个机场可能会经过多次,这违背了我们DAG的初心。
那到底什么是 一次性 的。
在这道题里,只有航班是一次性的了,将其设为点。
谁设为边,点与点之间的转移曰边,我们这里定义:同一架飞机 飞完一趟航班以后飞另一趟 ,这两趟航班之间就可以连边。
在什么条件下,一架飞机可以飞完一趟以后飞另一趟? 
在前一次飞完以后,能够在 下一趟开点 之前,赶到下一趟的 出发站 。我们就可以在这两趟航班之间连上边。
而这个判断里面,每一个需要的值都是可求的。
那么有人又要问了:可是题目并没有给出从一个机场赶到另一个机场所需的时间啊!
既然题目给了你这么多航班信息,你就不会用 $floyed$ 传递一下闭包 吗。
至此此题就转化成一道最小路径覆盖问题力。
套路六:虚点的构建:
这并不构成一种模型,但是这类型的题挺 多 的,所以单独开出来讲。
所谓虚点者,就是这并不代表某一个元素,而是代表一种 限制条件 或者 额外加成 。
比如我们说,如果有两个物品 $a$ 和 $b$ ,每个物品有两种状态 $1$ 和 $2$ ,每个状态有不同的价值。
同时,如果我们同时选了 $a1$ 和 $b1$ ,就可以额外获得值为 $c1$ 的价值;如果我们同时选了 $a2$ 和 $b2$ ,就可以额外获得值为 $c2$ 的价值。
首先我们需要创建一个虚点,代表 $c1$ 。
这时,因为我们有 “你可以选状态1,但你就选不了状态2了,这一切,值得吗” 。
所以我们应该上最小割!将所有状态 $1$ 连向源,所有状态 $2$ 连向汇!
其次,如果我们选择不割 $a1$ 和 $b1$ ,就能 保留 $c1$ 。
所以 $c1$ 与 “ $a1$ 和 $b1$ ” 不应站在割边的对立面上。而是当 能保留a1,b1的条件满足时,一样可以保留c1 。
胡乱 思考得知, $c1$ 应该是从源出来而流向 $a1,b1$ 的。
那建出全图就是这样:
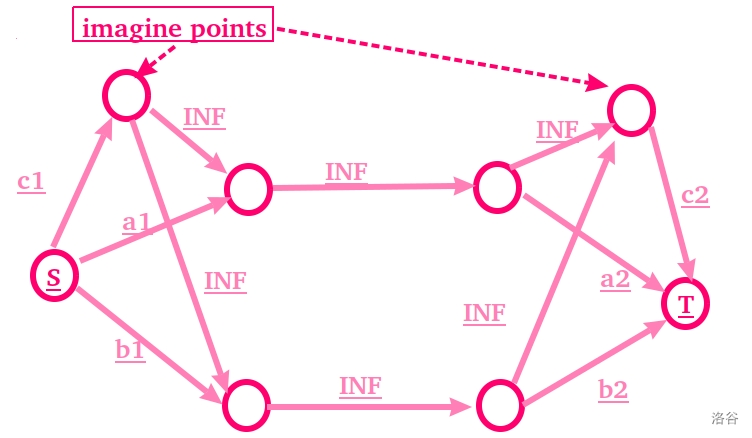
还挺好看。
手模几种情况即可验证这张图。
之后就是跑一个最小割的事。
可以看出,建立虚点的套路适用于 “集齐X个干员,组建幻神阵容,获得羁绊 buff” 的隔膜行为。
下面来康例题:
为甚么又是国集……
这道题的限制条件有亿点多,但是好在数据范围极小。
本着神仙 shadowice1984 “大了三分,小网络流;不小不大,斜率优化” 的箴言。我们尝试建图跑。
对于任意两个相邻的人,他们同选某一门会有额外 $buff$ ,这说明我们要建关于 $buff$ 的虚点。
之后的事就很简单了,对于每一种 $buff$ 都建虚点,最后跑最小割即可。
图过于气 势 恢 宏,这里就不放了。
代码放一下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
using namespace std;
const int LAR = 10000;
const int MAX = 5e5 + 7;
const int INF = 1e18;
/*网络流板子*/
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
int cur[MAX];
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
bool bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
memcpy(cur, head, sizeof(head));
return dep[T] != 0;
}
int dfs(int u, int in)
{
if (u == T || !in)
{
return in;
}
int out = 0;
for (int i = cur[u]; i; i = e[i].next)
{
cur[u] = i;
int v = e[i].to;
if (dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
if (!tmp)
{
continue;
}
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
if (in == 0)
{
return out;
}
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
/*几个数组分别对应该位置选文、选理、相邻都选文、相邻都选理*/
int A[107][107];
int B[107][107];
int C[107][107];
int D[107][107];
int N, M;
int idx(int x, int y)//取标号
{
return (x - 1) * M + y;
}
signed main()
{
cin >> N >> M;
int sum = 0;
S = 0, T = 5 * N * M + 1;
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> A[i][j];
sum += A[i][j];
adde(S, idx(i, j), A[i][j]);
adde(idx(i, j), S, 0);//文连源
}
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> B[i][j];
sum += B[i][j];
adde(idx(i, j), T, B[i][j]);
adde(T, idx(i, j), 0);//理连汇
}
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> C[i][j];
sum += C[i][j];
int u = 2 * N * M + idx(i, j);//虚点标号
adde(S, u, C[i][j]);//价值
adde(u, S, 0);
adde(u, idx(i, j), INF);//当然他自己也要选文
adde(idx(i, j), u, 0);
/*虚点连向四个方向的点*/
if (j - 1 > 0)
{
adde(u, idx(i, j - 1), INF);
adde(idx(i, j - 1), u, 0);
}
if (j + 1 <= M)
{
adde(u, idx(i, j + 1), INF);
adde(idx(i, j + 1), u, 0);
}
if (i - 1 > 0)
{
adde(u, idx(i - 1, j), INF);
adde(idx(i - 1, j), u, 0);
}
if (i + 1 <= N)
{
adde(u, idx(i + 1, j), INF);
adde(idx(i + 1, j), u, 0);
}
}
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> D[i][j];
sum += D[i][j];
int u = 4 * N * M + idx(i, j);//虚点标号
adde(u, T, D[i][j]);//价值
adde(T, u, 0);
adde(idx(i, j), u, INF);//当然他自己也要选理
adde(u, idx(i, j), 0);
/*向四个方向连边*/
if (j - 1 > 0)
{
adde(idx(i, j - 1), u, INF);
adde(u, idx(i, j - 1), 0);
}
if (j + 1 <= M)
{
adde(idx(i, j + 1), u, INF);
adde(u, idx(i, j + 1), 0);
}
if (i - 1 > 0)
{
adde(idx(i - 1, j), u, INF);
adde(u, idx(i - 1, j), 0);
}
if (i + 1 <= N)
{
adde(idx(i + 1, j), u, INF);
adde(u, idx(i + 1, j), 0);
}
}
}
int ans = 0;
while (bfs())
{
ans += dfs(S, INF);
}
cout << sum - ans << endl;//总价值-最小割
}
1 |
|
套路七:二分与枚举:
有的题目,他条件一点都不 给 ,或者他 给 得不够多。
如果我们用传统的套路,我们会寸步难行。
这时,我们如果尝试用 枚举/二分 的做法,相当于自己凭空创造了一个条件,这样我们就可以完成一些 板子的套用 模型的构造。
我们可以根据这个条件来建图跑,如果跑出的答案不满足要求,则 调整图的形态 再跑。
我们有时只需要改动一些边的参数,但像我这种蒟蒻只会大力重新建图。(这就是我常数特别大的原因之一)
_有关更优秀地改动边,这里埋下一个伏笔。_
您是否还记得之前的一道《魔术球问题》,那题中,我们不断放新球的过程,实际上就属于套路七中的 枚举 环节。
这一套路思想就这,重在运用。
劲爆例题
这题说要让“最多的最少”,想到了二分。
赢最多的人赢多少场,这是有边界的。
我们就可以随手二分赢最多的人的胜场。
那图呢?
我们看到,一场比赛只能有一个 人赢 。(雾)
所以表示比赛的点向参与的两者各连 流量为 1 的边。源点向所有比赛连 流量为 1 的边。
而我们二分到一个人最多赢 $mid$ 场。也就是一个人连向汇点最大为 $mid$ 。
跑出最大流如果 $\geq$ 比赛数,说明是 可行的 。尝试用更小的 $mid$ 。
最终会二分出一个答案。
输出方案就看比赛连向谁的那条边是满流即可,谁是满流谁是人赢.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
using namespace std;
const int MAX = 5e5 + 7;
const int INF = 1e18;
/*dinic组件*/
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
int cur[MAX];
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
bool bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
memcpy(cur, head, sizeof(head));
return dep[T] != 0;
}
int dfs(int u, int in)
{
if (u == T || !in)
{
return in;
}
int out = 0;
for (int i = cur[u]; i; i = e[i].next)
{
cur[u] = i;
int v = e[i].to;
if (dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
if (!tmp)
{
continue;
}
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
if (in == 0)
{
return out;
}
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
int N, M;
int a[MAX], b[MAX];
int akioi[MAX], tot = 0;//akioi 数组记录(表示 “这场比赛流向参赛者” 的边)的编号
/*二分函数*/
bool judge(int x)
{
memset(head, 0, sizeof(head));//暴力清空
eid = 1;
S = 0, T = 20000 + N + 1;
/*建边*/
for (int i = 1; i <= M; i++)
{
adde(S, i, 1);
adde(i, S, 0);//源连向比赛
adde(i, a[i] + 20000, 1);
akioi[i] = eid;
//记录下这条边的编号,以后输出方案要用
adde(a[i] + 20000, i, 0);
adde(i, b[i] + 20000, 1);
adde(b[i] + 20000, i, 0);//比赛连向参赛者
}
for (int i = 1; i <= N; i++)
{
adde(i + 20000, T, x);
adde(T, i + 20000, 0);//参赛者连向汇
}
int ans = 0;
while (bfs())
{
ans += dfs(S, INF);
}
if (ans >= M)
{
return 1;
}
return 0;
}
signed main()
{
cin >> N >> M;
for (int i = 1; i <= M; i++)
{
cin >> a[i] >> b[i];
}
/*二分*/
int l = M / N, r = M, ans = M;
while (l < r)
{
int mid = (l + r) >> 1;
if (judge(mid))
{
r = mid;
}
else
{
l = mid + 1;
}
}
cout << l << endl;
//以这个数为答案再跑一遍,生成方案
judge(l);
for (int i = 1; i <= M; i++)
{
if (e[6 * (i - 1) + 4].val == 0)//查询其是否满流
//(若流向一个人的边的容量变成了0,则它满流)
{
cout << 1 << endl;
}
else
{
cout << 0 << endl;
}
}
}
1 |
|
套路INF:其他不常见技巧
- 拓扑去环:
试想如果我们建出来的图中有环,跑网络流会得到什么结果。
可能是 $RE$ ,可能是 $TLE$ ,可能是 $WA$ ,总之跑不出正确答案。
有的题目中,环是可以被直接忽略的。这时我们就可以先跑 拓扑排序 ,把环找出来,在之后建模时直接忽略即可。
比如下面这道题:
首先,这题基础建模思路就很难想到。(毒瘤题实锤)
对题目中的题意一通抽丝剥茧,我们发现,一个植物要能被吃,需要满足这两个前置条件。(看图)

它右边的都被吃完了(参考这里的大嘴花在坚果墙左边导致不能被吃)。
能攻击到这一位置的植物都被吃完了 (参考这里的坚果墙的位置被大嘴花攻击导致不能被吃
停,你刚刚说了 “前置” 是吧。
然后 最大权闭合子图 的模型不就呼之欲出了?
植物 $i$ 的价值设为 $val_i$ ,正权连源,表示收益,负权连汇,表示花费。
如果一个植物 $j$ 保护着 $i$ , $i$ 向 $j$ 连边 (这里包含了 j 在 i 右侧 和 j 攻击到 i 的位置 两种情况)
答案就是跑出的总的最大收益。
然后,我们会发现一个残酷的事实,如果你是僵尸,大嘴花和坚果墙你一个都吃不到。(惨)
他们互相保护,在我们建出的图上就形成了一个环。如果我们直接跑会爆炸。
这时我们就需要 拓扑去环 了。
在建网络流模型之前,我们需要反向建一张图,能被遍历到的结点证明它不在环上,我们用这种点再来建我们用来跑网络流的图。
之后跑最大权闭合子图即可。
- 退流:
_伏笔消除_
如果我们要在一张跑完网络流的图上,稍作删边,再跑下一次网络流的话,我们可能要暴力重建。
但是其实这并不需要这么高的复杂度, 退流 就是一种高效解决删边重跑的方法。
笔者突然对自己的认知产生了迷惑,先咕。
那网络流部分就告一段落辣。
杜教筛
sto $\color{black}{\texttt{M}\color{red}{\texttt{iFaFaOvO}}}$ orz
杜教筛是一种高端筛法,用以快速处理积性函数的前缀和。
以前 $\color{purple}{\texttt{给}}$ 指导讲过这一高端科技,但是那时候的我连数论分块都没搞清楚,更别说杜教筛了。
昨天入的坑,今天来整理一下 $QvQ$ 。
原理?
假设我们要来筛一个函数 $f$ 。
我们设另一个积性函数 $g$ ,然后把他们俩 卷 起来,得到一个 $h$ 。
也就是 $f*g=h$ 。
再设一个 $sumf$ 表示 $g$ 的前缀和。
以上是杜教筛的一些弹药。
关于 $h$ 的前缀和,展开做钬钊氪镭 卷 积的形式有:
当前的这个式子启发我们,当我们易求 $h$ 的前缀和时,只需获得一个 $sumf(\lfloor\frac{n}{d}\rfloor)$ ,就能光速整除分块推知 $sumf(n)$ 。
数论函数的选择
随缘乱凑(不是)
回归算法本身,我们需要的 $g$ ,要求是和 $f$ 卷 起来以后得到一个易求前缀和的 $h$ 。
所以我们需要通晓一些互 卷 关系:
$\mu*1=\epsilon\quad$这个很simple吧,$\mu$ 的一条性质
$\varphi*1=id\quad$ 这个看上去也很simple,$\texttt{\color{black}{R}\color{red}{ui_R}}$神写过一篇文章证过。
$\muid=\varphi\quad$ 上一条柿子佐佑同 *卷 $\mu$ 即可
$f(i)=\sum_{i}^{n}(i\cdot\varphi(i)),fid=n^2\quad$ 卷 积拆开来发现会把$f$ 里的 $i$ 消掉得 $\sum_{d|n}n\cdot\varphi(d)$,然后套 $\varphi1=id$
$f(i)=\sum^n_i(i^k\cdot\varphi(i)),f*id=n^{k+1}\quad$ 上一个柿子的一个推论
劲爆例题
- 【模板】杜教筛(Sum)
首当其 冲 的必然是模板。
题目要求 $\mu$ 和 $\varphi$ 的前缀和,我们分别来思♂尻一番。
思♂尻用什么东西来 卷 $\mu$ ,要求和 $\mu$ 卷 完以后要得到一个 易于计算前缀和 的氡氡。
通过 翻博客 慎重考虑后,我们选择用 $1$ 去 卷 它,因为 $\mu*1=\epsilon$ ,而 $\epsilon$ 的前缀和必然是 1。
所以瑇入 $g=1,h=\epsilon$ 我们有:
这样我们就解决了 $\mu$ 。
那 $\varphi$ 呐?
其实也很套路,因为 $\varphi*1=id$ ,而 $id$ 的前缀和,高斯哥哥已经帮我们推出公式了,是 $n\cdot(n+1)\div2$ 。
所以瑇入 $g=1,h=id$ 我们有:
下面是瑇码,具体实现细节在注释:
1 |
|
_PS:小心爆精(不然就像我一样的下场)_
*象棋与马
题面要素溢出。
不难发现,如果一种跳跃规则是可达所有点的,那么它唯一的要求就是有能力达到 相邻格,如 $(0,0)$ 达到 $(0,1)$ 。
我们意识到,这一步骤其实相当于能否从 $(0,0)$ ,向各个方向瞎jb跳一跳,最后达到 $(0,1)$ 。
设我们一步能跳 $(x,y)$ ,那么 本质不同 (唐突本质不同)的行走方案有四种:
(在纵轴上走负方向其实可以看作走负数次正方向)
那么我们有:
也就是说我们瞎跳过程中,有 $a$ 次 $(x,y)$ 的跳跃, $b$ 次 $(y,x)$ 的跳跃, $c,d$ 同理。
开始 $\mathbf{dark}$ 力合并两个柿子,提出 $x,y$ 来。
设 $a+b=A,c-d=B$ ,转化式子
格物致知这个柿子,我们意识到 $x,y$ 一定得 互质 (一旦二者有非1的公约数,则结果必然 也有 这个公约数)。
此外,二者必须 奇偶性互异 ,否则结果 必然为偶 。
因此,二者必然一奇一偶。
设此时答案是 $f(x)$ ,先记着,因为我们限定了 $x$ 的奇偶性,相当于砍掉了一半的答案,所以最后答案 $ans(x)=2\cdot f(x)$。
抓~紧~时~间~容~斥~
他欧拉反 演 起来了:
因此,我们收获了一个看上去很彳亍的式子,但这还不够,$x\leq10^{11}$。
提出一个 $\varphi(i)$ 来:
后半段可以 杜教筛 ,前半段 递归求解 即可。
按 $\color{purple}{\texttt{给指导}}$ 的话说,这种“自递归函数”是未来数论出题的热点。
(这并不影响数论毒瘤爪巴)
瑇码:
1 |
|
咕咕咕!
最后更新: 2021年08月03日 10:16
