推一下蒟蒻 $\color{salmon}{blog}$ 233~
这是一道小思维题,有趣还是挺有趣的。
题意见此 ,这里不赘述。
我们都知道,一个置换可以拆成许多个不相交的循环的并,比如 $(^{1\ 2\ 3\ 4} _ {4\ 2\ 1\ 3})$ 就可以拆成 $(^{1\ 3\ 4} _ {4\ 1\ 3})$ 和 $(^{2} _ {2})$ 。
也就是说,因为每个循环是不相交的,所以我们只要确认 每个循环 是否都能作为一个合法的 两次置换后的情形 。
怎么确保呢,这里有一个小力分讨。
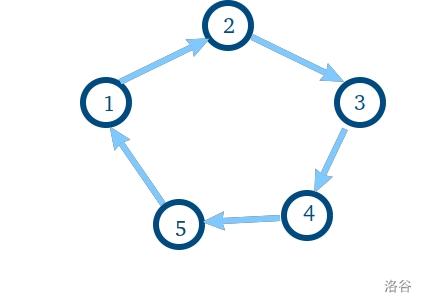
如果这是两次置换后的情形,是一个循环, $i$ 指向 $i+1\pmod n$ 。
那么我们如何构造出这种置换呢。
认真思尻我们可以构造出这样的氡氡:
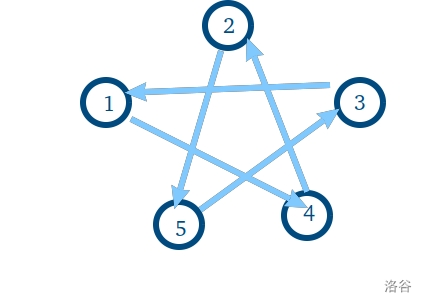
我们使 $i$ 指向 $i+\dfrac{n+1}{2}\pmod n$ ,由此一来,两次置换后,$i$ 就指向了 $i+n+1\pmod{n}$ ,也就是 $i+1\pmod n$ ,那么就是一个循环的形状了~
换一种解释,我们其实是要构造一种循环移位,使得两次循环移位的总距离 $\equiv 1\pmod n$
这个构造策略可以推广到所有 奇数循环 上,即:
『构造置换为( $i$ 指向 $i+\dfrac{n+1}{2}\pmod n$ ) ,两次置换后可得到该循环。』
那么我们可以说,所有奇数循环都是 合法 的两次置换后的情形了。
我们把一个偶数循环整出来看一看:
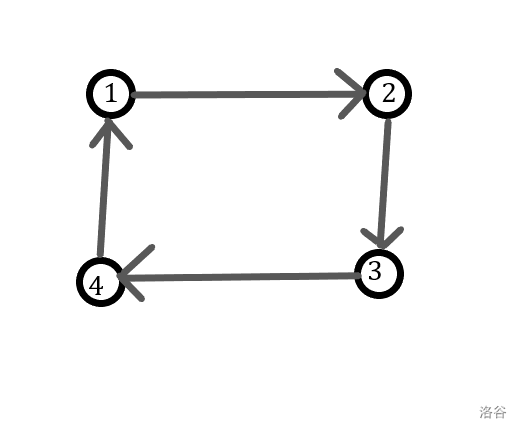
我们发现,任何循环移位都不能使两次移位总距离 $\equiv 1\pmod n$ ,因为 $kn+1$ 是一个奇数而总距离一定为偶。
那么奇数时的构造策略在这里就不适用了,我们想想别的方法。
如果原来是这样一张图:

移位两次后就变成了这样:
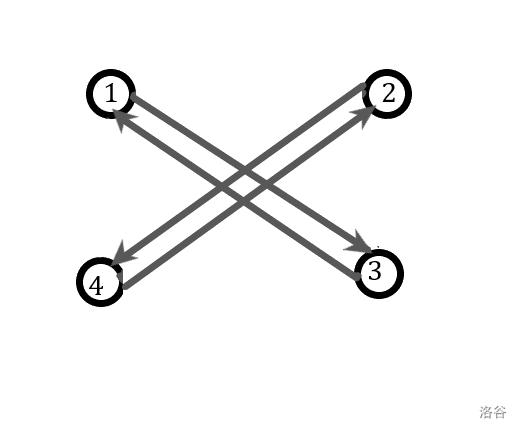
我们发现,如果一个偶数环一开始是 ( $i$ 指向 $i+1$ )的话,移位两次后原图就会裂开成两个大小为 $\dfrac{n}{2}$ 的环。
而我们要造偶数环,也只有这一种方法了。
那么我们就可以稍作整理了:
首先,找出最终形态里的所有环。
其次,其中奇数环我们全都可以就地构造,偶数环我们只能通过 大环分裂 得来。那么也就是说,我们所有的偶数环都得是 成对 出现的。
这个很好办,只要为环的大小开个桶,最后查桶内个数 是奇是偶 即可~~~
这里是瑇码qwq(写的很丑,但是至少能看?):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int MAX = 1e2 + 7;
const int MOD = 1e9 + 7;
void print(bool a)
{
cout << (a ? "Yes" : "No") << endl;
}
int N;
int tong[MAX];
int vis[MAX];
char S[MAX], T[MAX];
char AKIOI[37] = " ABCDEFGHIJKLMNOPQRSTUVWXYZ";
vector<int> v;
signed main()
{
int t;
cin >> t;
while (t--)
{
cin >> S + 1;
v.clear();
memset(vis, 0, sizeof(vis));
memset(tong, 0, sizeof(tong));
memcpy(T, AKIOI, sizeof(AKIOI));
for (int i = 1; i <= 26; i++)
{
if (vis[i])
{
continue;
}
char tmp = S[i], pos = i;
int flag = 0;
int cnt = 0;
while (S[pos] != tmp || flag == 0)
{
cnt++;
flag = 1;
for (int j = 1; j <= 26; j++)
{
if (S[j] == T[pos])
{
pos = j;
break;
}
}
vis[pos] = 1;
}
if (cnt % 2 == 0)
{
tong[cnt]++;
if (tong[cnt] == 1)
{
v.push_back(cnt);
}
}
}
int M = v.size();
int fl = 1;
for (int i = 0; i < M; i++)
{
if (tong[v[i]] % 2 != 0)
{
print(0);
fl = 0;
break;
}
}
if (fl)
{
print(1);
}
}
}
|





