$\color{salmon}{\texttt {放小球:}}$
$n$ 球, $m$ 盒
| 小球是否不同 | 盒子是否不同 | 是否允许空盒 | 相应做法 |
|---|---|---|---|
| $\surd$ | $\surd$ | $\surd$ | $m^n$ |
| $\surd$ | $\surd$ | $\times$ | $m!\cdot {\small\texttt{斯二林}}(n,m)$ |
| $\surd$ | $\times$ | $\surd$ | $\sum_{i=1}^{m} {\small\texttt{斯二林}}(n,i)$ |
| $\surd$ | $\times$ | $\times$ | $\small\texttt{斯二林}(n,m)$ |
| $\times$ | $\surd$ | $\surd$ | $C_{m+n-1}^{n}$ |
$\times$|$\surd$|$\times$| $C_{n-1}^{m-1} $
有关斯二林:
$S(N,M)=M\cdot S(N-1,M)+S(N-1,M-1)$
对于该式理解:
有如今已有 $N$ 个球,放置在 $M$ 个盒中。我们是通过放置第 $N$ 球来达成的这一状态。
能转移到这里的有两种情况。
其一:放这个球是在已经放有球的盒子里,这样的话,盒子数没变过,有 $M$ 个。也就是由 $S(N-1,M)$ 转移来,又考虑到第 $N$ 球有 $M$ 个盒子可以放,故需乘上 $M$ 。
其二:放这个球的时候是新开了一个盒子,这样新盒子数是加 $1$ 得来。也就是由 $S(N-1,M-1)$ 得来。
二者结合即有上式。
对第五行的理解:
设第 $i$ 个盒子内球数为 $a_i(a_i\geq 0)$ 可看作是求 $a_1+a_2+\cdots +a_m=n$ 的非负整数解的组数。
求这样的方程的非负整数解的组数的算式为: $num=C^{n}_{m+n+1}$ ,故可将该方法迁移到此处。
对第六行的理解:
插板法天下第一!
看作是 $n$ 个球,现要插板将其分成 $m$ 块即可。
那就有 $n-1$ 个间隙,需插 $m-1$ 块板。 $n-1$ 选 $m-1$ ,有 $C^{m-1}_{n-1}$ 种方法。
$\color{salmon}{\texttt {期望次数:}}$
格式:
对XXX(哈希表/有序数组/链表)进行XXX(二分查找/线性探测),等概率情况下,(成功/失败)的(平均查找长度/平均比较次数)为___
。
| 这是什么 | 要求什么 | 怎么做 |
|---|---|---|
| 哈希表 | 线性探测的平均探测次数 | $1+\dfrac{\small\texttt{出现冲突的次数之和}}{\small\texttt{元素个数}}$ |
| 哈希表 | 查找成功的平均次数 | 同上 |
| 哈希表 | 查找失败的平均次数 | (下方特讲) |
| 有序数组 | 二分查找的平均次数 | 分数形式:分子的递推式为 $D_i=D_{i-1}+\lfloor\log_{2} i\rfloor+1$ ,其中 $D_1$ 为 $1$ 。分母为元素个数。 |
哈希表查找失败的平均次数:
这里有一种非常易于实现的方法,先把线性探测完了以后的哈希表写下来如这样。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 7 | 14 | 空 | 8 | 空 | 11 | 30 |
我们要查一个元素,会先看看它本该对应的位置是否有它。
倘若没有,我们会怀疑它是不是因为冲突而顺延了,于是到下一个位置找它。
一直找到一个空位置,我们就可以宣告查找失败了。
可见,查找失败的平均次数和我们 怀疑顺延 的次数有关。
于是,我们可以把一个位置 直到下一个空位的距离 先直接一眼看出,写在数组下方。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 7 | 14 | 空 | 8 | 空 | 11 | 30 |
| 2 | 1 | 0 | 1 | 0 | 2 | 1 |
但是这只是我们怀疑的次数,我们一开始查它 本该对应的位置 的时候其实也应该算一次查找。所以每一位加一:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 7 | 14 | 空 | 8 | 空 | 11 | 30 |
| 3 | 2 | 1 | 2 | 1 | 3 | 2 |
再把下面这些加起来,除上元素个数即可。
为什么查找成功的次数和平均探测次数是一样的:
其实两者中我们的动作可以看作是一样的,都是先查本位,往下找直到一个可以还没有被占用的位置。
有关二分查找的次数:
这个递推式是刚刚花 $5min$ 推出来的,不好证明。
直接定址法是完美哈希
$\color{salmon}{\texttt {进制相关:}}$
X进制转十进制——加权法:
十进制转X进制——短除法:
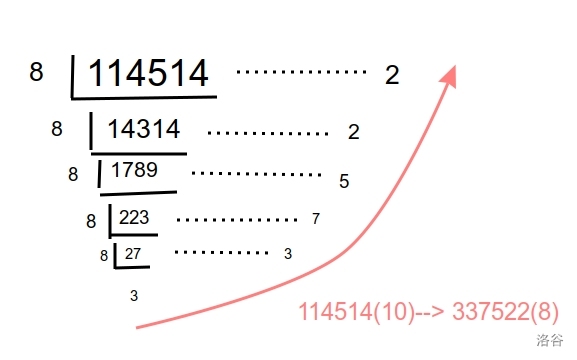
除以 $base$ 取模,倒序拼接成一个数。
X进制小数转十进制:
十进制小数转X进制:
短乘法,乘 $base$ 取整数部分,正序拼接成一个数。
任意的十进制有限小数,未必也是八进制有限小数。
$\color{salmon}{\texttt{ccf}}\color{salmon}{\texttt{赞歌:}}$
NOI全称:全国青少年信息学奥林匹克竞赛。
今年是第 32 届IOI,中国队获得了 4 金。
1984年,邓小平 指出:“计算机的普及要从娃娃做起。” CCF 于 1984 年创办全国青少年计算机程序设计竞赛(简称:NOI)。故今年是第 37 届,在 长沙 举行。
NOIP的创办时间:1995 年,故今年是第 26 届。
2020年 开始, 除NOIP以外 的NOI系列其他赛事(包括冬令营、CTSC、APIO、NOI)将不再支持 Pascal语言和C语言;
从 2022年 开始,NOIP竞赛也将不再支持 Pascal语言 。即以后只有 C++ 一个了。
竞赛费:0元 。但本着 谁受益谁承担成本 原则,参加竞赛所需的餐饮、住宿、交通、保险等费用由参加者自行承担。
2011年 起,复赛提高组由 一试改为两试 ,分由两天进行。每天竞赛试题由原来的 4题改为3题 。
第一届 APIO 于 2007 年在 澳大利亚 举办。中国第一次承办是在 2010 年。
第一届 NOI 网络同步赛于 1999 年举办。
$\color{salmon}{\texttt{图论相关:}}$
| 概念 | 定义 | 判定 |
|---|---|---|
| 欧拉通路 | 过图中所有边 恰好一次 且 行遍所有顶点 的通路 | 1.连通 2.恰有 0个或2个 奇度顶点 |
| 欧拉回路(欧拉闭迹) | 过图中所有边 恰好一次 且 行遍所有顶点 的回路 | 1.连通 2. 无 奇度顶点 |
| 哈密顿通路 | 过图中所有顶点 恰好一次 的通路 | 对于每对不相邻点,$d(u)+d(v)\geq N-1$ ($N$ 为顶点数, $d$ 为度数) |
| 哈密顿回路 | 过图中所有顶点 恰好一次 的回路 | 所有顶点的度数大于等于 $\frac{N}{2}$ ($N$ 为顶点数) |
二分图|能把顶点分成两个集合,且两个集合 内部没有边 的图|没有 奇环的图
有关欧拉回路和欧拉通路:
实则可理解为是 从任意一点都能一笔画全图 还是 得从某个特定的起点开始才能一笔画全图 。
有关欧拉回路和哈密顿回路:
欧拉回路:需一笔经过全边。
哈密顿回路:只需一笔能串起所有节点即可。
$\color{salmon}{\texttt{存图方式:}}$
$N$ 点, $M$ 边, $d$ 为一点出度。
| 存图方式 | 遍历一点出边 | 遍历全图 | 查询单边 | 跑拓扑/ $dfs$ 效率 |
|---|---|---|---|---|
| 邻接矩阵 | $O(N)$ | $O(N^2)$ | $O(1)$ | $O(N^2)$ |
| 邻接表 | $O(d(N))$ | $O(M)$ | $O(d(N))$ | $O(N+M)$ |
| 链式前向星 | 同上 | 同上 | 同上 | 同上 |
为什么邻接表和前向星一样:
因为前向星就是一种邻接表。
邻接矩阵中的无效元素个数:有向: $N^2-M\;$ 无向:$N^2-2M$
$\color{salmon}{\texttt{树相关:}}$
题型一:
在一棵树中,度为 $1$ 的结点数有 $a_1$ 个,度为 $2$ 的结点数有 $a_2$ 个, $\dots\dots$ ,度为 $n$ 的结点数有 $a_n$ 个,则度为 $0$ 的结点数为()个。
树上的度数指的是其出度。可理解为度为 $K$ 的结点会贡献出 $K$ 个出度。而除根结点外,每个结点都会消耗掉一个出度。要求最后出度消到 $0$ 。则有:
$a_0\cdot 0+a_1\cdot 1+\cdots +a_n\cdot n-(a_0+a_1+\cdots+a_n-1)=0$
被减数即贡献出的出度之和,减数即消耗掉的出度之和(这里减 $1$ 是因为根结点不消耗出度)。
题型二:
一棵 $K$ 叉树的结点数为 $N$ ,则它的最小高度为()。(设根结点深度为 $1$)
$K$ 叉树,则第 $x$ 层最多有 $K^{x-1}$ 个结点。
前 $x$ 层就最多有 $\lfloor\dfrac{K^x}{K-1}\rfloor$ 个结点。
则在最后一个结点之前高度就有 $\lfloor\log_{K}N(K-1)\rfloor$ 层。
那他这一层就是第 $\lfloor\log_{K}N(K-1)\rfloor+1$ 层。
_其他的题型都还简单(bushi)_
先序序列和中序序列相同的二叉树的特征为:空树 或者 任一结点均无左孩子的非空二叉树
中序序列和后序序列相同的二叉树的特征为:空树 或者 任一结点均无右孩子的非空二叉树
先序序列和后序序列相同的二叉树的特征为:空树 或 仅有一个结点的二叉树
$\color{salmon}{\texttt{刚学的几个式子(还不会证):}}$
$\sum_{i=1}^{n} i^3=\dfrac{n^2(n+1)^2}{4}$
$\sum_{i=1}^{n} i^4=\dfrac{n(n+1)(2n+1)(3n^2+3n-1)}{30}$
错排:$D(n) = n! [(-1)^2/2! + … + (-1)^{n-1}/(n-1)! + (-1)^n/n!]$
$\color{salmon}{\texttt{计算机知识:}}$
冯诺伊曼的计算机结构的核心思想:
单处理机结构,机器以运算器为中心;
采用程序存储思想;
指令和数据一样可以参与运算;
数据以二进制表示;
将软件和硬件完全分离;
在微机系统中,最基本的输入输出模块BIOS存放在 ROM 里。
想不到吧,RAM 和 外存 也是 输出 设备!
显存断电后是 不会 保存的。
存储程序工作原理的特点是: 事先编制程序 和 从存储器中依次取出程序自动执行
Fortran 是历史上的 第一种 高级语言,它面向 科学计算
Simula 67 是历史上的第一个支持 面向对象 的语言
Smalltalk 是历史上的第一个 完善的 支持 面向对象 的语言
根据汉字国际GB2312-80的规定,一个汉字的内码码长为 16 bit
汉字区位码 $+2020(H)$ 得国标码,国标码 $+8080(H)$ 得机内码。
一级汉字以 拼音 排序,二级汉字以 偏旁部首 排序
图像分辨率指图像中存储的 信息量
显示分辨率是显示器在 显示图像 时的分辨率
调色板中的颜色数依 颜色深度 而定
$\color{salmon}{\texttt{排序相关:}}$
时间复杂度分类:
| $\qquad n^2\qquad $ | $\qquad n\log n\qquad $ | $\qquad n\qquad $ | $\qquad$ 奇怪的复杂度$\;$ |
|---|---|---|---|
| 冒、插、选 | 归(严格)、堆(严格)、快(最优 $O(n)$ ,最劣 $O(n^2)$ ) | 桶 | 计 ( $O(n+w)$ ,$w$ 为值域),希尔(最优 $O(n)$ ,最劣 $O(n\log^2 n)$,基 |
_注:也有称希尔平均为 $O(n^{1.5}$)的说法_
稳定性分类:
| $\qquad$稳定$\qquad$ | $\qquad$不稳定$\qquad$ |
|---|---|
| 插、冒、计、归、基、桶 | 选、堆、快、希 |
即:
$n^2$ 除选择都为稳定。
$n\log n$ 除归并都为不稳定。
$n$ 都为稳定。
就地性分类:
| $\qquad$就地$\qquad$ | $\qquad$不就地$\qquad$ |
|---|---|
| 插、选、冒、希、快、堆 | 归、计、基、桶 |
_注:有的写法的归并是就地的_
即:
$n^2$ 都为就地。
$n\log n$ 除归并都为就地
$n$ 都为不就地。
其他知识:
C++ 的 $\operatorname{sort}$ 在数据较小的时候能自动转换为 堆排
希尔排序的最后一趟是 插入排序 ,因为希尔本质上就是插入排序的优化算法。
数据几乎有序时:插入、希尔、归并、冒泡 快于 快排
平均 比较次数最少 的是快排。
求第 $k$ 大最低的算法时间复杂度为 $O(n)$ ,由 快排 思想实现。
堆排天下第一!(bushi
优先级:
$(\; ) > \lnot > \bigwedge > \bigvee$
最后更新: 2021年04月17日 16:11

